过去一段时间里小编一直接触启发式算法,自从学习了运筹学以后,就对运筹学的精确方法垂涎已久,像什么单纯形法啦,分支定界啦,割平面啦…… 就在小编一边做梦一边睡大觉的时候,boss发来一个任务:用Gomory割平面法求解混合整数规划问题。于是小编马上从床上跳起来,挑灯夜战为大家整出了这个代码…
内容提要:
1、混合整数规划问题
2、单纯形法和对偶单纯形法
3、割平面法
4、割平面法Java实现
什么是混合整数规划
混合整数规划问题(Mixed Integer Programming,MIP)属于线性规划的一种。关于线性规划,过去的推文里我们有介绍过,还不懂的同学可以参考这篇推文:
运筹学教学|十分钟快速掌握单纯形法(附C 代码及算例)
整数规划,顾名思义,就是优化问题里的变量要求取整数。比如老板们要雇佣咱们打工人,只能雇佣整数个,不能雇半个。混合整数规划,就是决策变量即有整数又有小数,比如买西瓜,可以买半个,也可以买一个、两个。
在线性规划模型中,我们直接用“整数”两个大字来描述这种约束。

解决整数规划问题要比解决一般线性规划问题困难得多,因为整数部分的处理无法用简单的大于、小于号描述,只能简单粗暴的检查解是否有小数部分。现在还没有已知的多项式时间算法来解决广义的MILP问题。
常见的解决MIP的方法有分支定界法和割平面法。有关分支定界法可以看这些推文的介绍:
干货 | 10分钟带你全面掌握branch and bound(分支定界)算法-概念篇
干货 | 10分钟搞懂branch and bound算法的代码实现附带java代码
运筹学教学|分枝定界求解旅行商问题
单纯形法和对偶单纯形法
在介绍割平面法前,我们还要介绍两种基本方法:对偶单纯形法和单纯形法。
有关单纯形法,也是很基础的知识啦,不懂的照惯例回去看上面的推文。
这里小编简单介绍下对偶单纯形法。
对偶单纯形法是用来补充纯粹的单纯形法无法解决特殊问题的缺陷。而且对偶单纯形法更加“强大”,因为它可以在等式右端(b)为负值时直接求解,这也是选择使用它的大多数场景。
我们直接用这个例子来看:
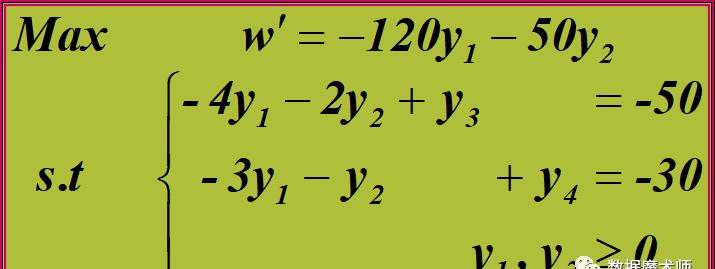
单纯形法当然还是有单纯形表,不过在新的单纯形表中,本来在右侧的theta栏变到的下侧。
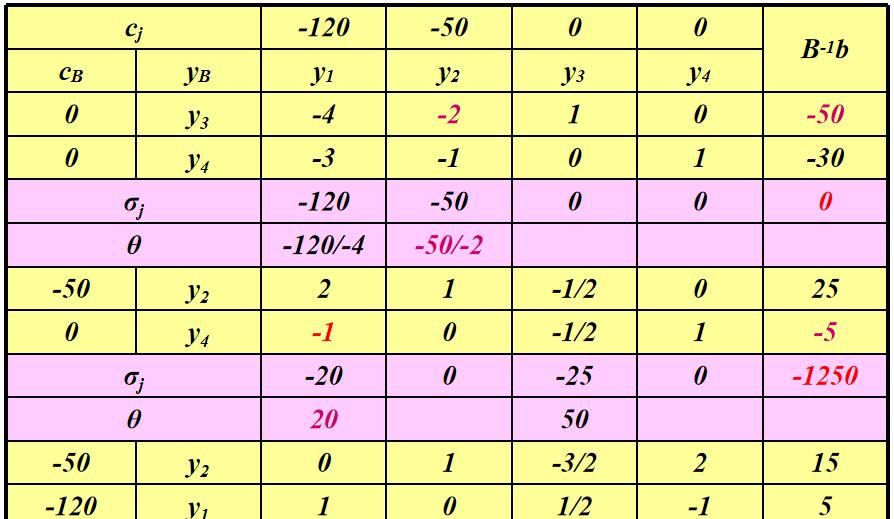
每次更新单纯形表时,我们先从最右侧的B^-1b一栏找到最小的负数(如果都为正数,则最优解以找到),确定为第y行;第二,依照单纯形法的方法更新检验数;第三,对第y行的所有小于0的数,计算theta = 检验数 / 对应的y值,取最小的theta,记为第x行。最后,用单纯形法同样的方法,将x列对应的变量入基,y行对应的变量出基。
不断迭代,知道所有B^-1b都大于0。
怎么样,是不是很简单呢~

割平面法
无论是分支定界还是割平面法,解决整数约束的方法只有一个:“看”解中的变量是否为整数。
分支定界和割平面法利用各自的方法不断增加约束、缩小解空间,再通过单纯形法得出新的解空间下的最优解,最后判断新解是否为整数,不是则继续迭代。

Gomory割平面法利用每次新解里的非整数部分得到一个新的不等式。具体如何获得这个不等式,且看小编用一个例子来说明:
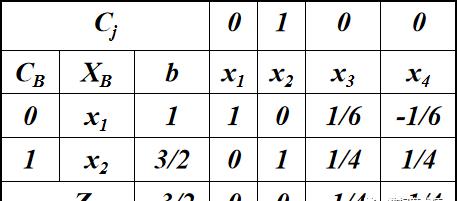
上面是一个线性规划问题的单纯形表终表,可以看到x_2目前取值为3/2,不是整数,因此我们对这一行进行如下处理:
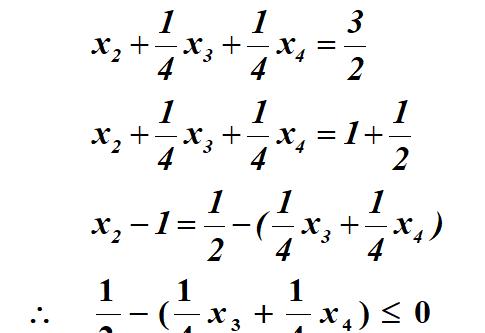
我们把式子左右两端的小数部分和整数部分分开(注意小数部分是大于0的),再将整数部分移项至左侧,小数部分移项至右侧。由于等式右侧为小数-整数的形式,又因为从等式左边看,式子的答案是整数,所以等式的值必定≤0。
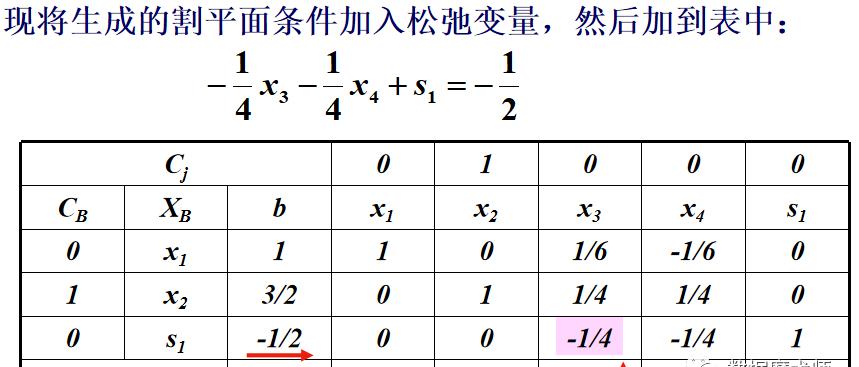
最后将新的约束加入单纯形表中。由于新约束的整数部分≤0,所以利用对偶单纯形表进一步求解,依次类推直到所有变量都为整数。
必须要注意的是,Gomory割平面法要求输入的初始不等式左右两端系数必须为整数,这是为了保证上述割平面满足符号要求。对于非整数部分,可以通过等式左右两端同时乘以分母的公倍数来预处理。
割平面法代码分享
怎么样,学习完新算法之后是不是蠢蠢欲动想要看代码了呢?

代码分为Main、Data、Algorithm三个类,其中Main是主函数入口,Data存放线性规划问题、单纯形表的内容,Algorithm则是我们的单纯形法、对偶单纯形法和割平面法的算法。
一些变量:
public int variableNr; // 变量个数 public int constraintNr; // 约束方程个数 public ArrayList<ArrayList<Double>> A; // 约束方程系数 public ArrayList<Double> b; // 自由变量 public ArrayList<Double> c; // 目标函数系数 public ArrayList<Integer> xB; // 基变量 public ArrayList<Double> theta; // 单纯形表右侧theta public ArrayList<Double> dualTheta; // 对偶单纯形表下侧theta public ArrayList<Double> o; // 检验数 public ArrayList<Boolean> isInteger; // 是否是整数 public int solution; // 0代表已为最优解且最优解唯一;1代表继续迭代;2代表不存在最优解;3代表最优解不唯一
三个算法的框架:
// 单纯形法 private void simplexAlgorithm() { initialSimplex(); while (!pivot()) { printSimplexTable(); Gaussian(); } } // 对偶单纯形法 private void dualSimplexAlgorithm() { while (!dualPivot()) { printSimplexTable(); Gaussian(); } } // 割平面法 public void gomoriAlgorithm() { simplexAlgorithm(); while (!checkIsOver()) { int y = findMaxFractionalPart(); addRestriction(y); dualSimplexAlgorithm(); } }
简单介绍几个重要的函数。privot函数和dualPrivot函数是单纯形法和对偶单纯形法中计算检验数、theta值以及寻找入基、出基变量的函数;Gaussian函数进行入基和出基变换后的高斯消元变换;printSimplexTable函数在控制台中打印单纯形表;addRestriction函数在单纯形表中加入新的约束条件(割平面)。
具体代码比较长,小编就不都放出来啦,感兴趣的同学可以在文末下载代码仔细查看。
最后补充一句,由于编写代码使用的是Java语言而不是专门的数学运算语言,计算过程中会有很多机器误差(比如1变成1.000000004),小编简单处理了一部分,可还是会影响算法。同时,面对一些复杂的算例,算法可能会出现一直跑不出结果、或者速度很慢的情况,请大家以学习的眼光对待这份代码(不要一个算例跑不出来就一直戳小编啦),真正需要求解还是祭出我们的求解器吧。
再强调一下,不等式的所有系数必须为整数!否则后果自负!
输入的算例可以在文末下载,为了简化代码,我们这里要求输入带单位矩阵的标准式。
运行结果:
算例输入:

输出单纯形表:
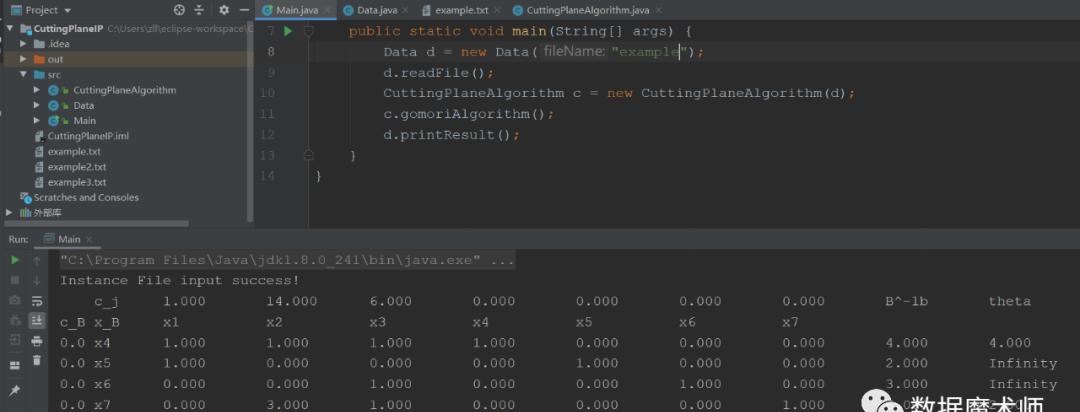
输出最优解:
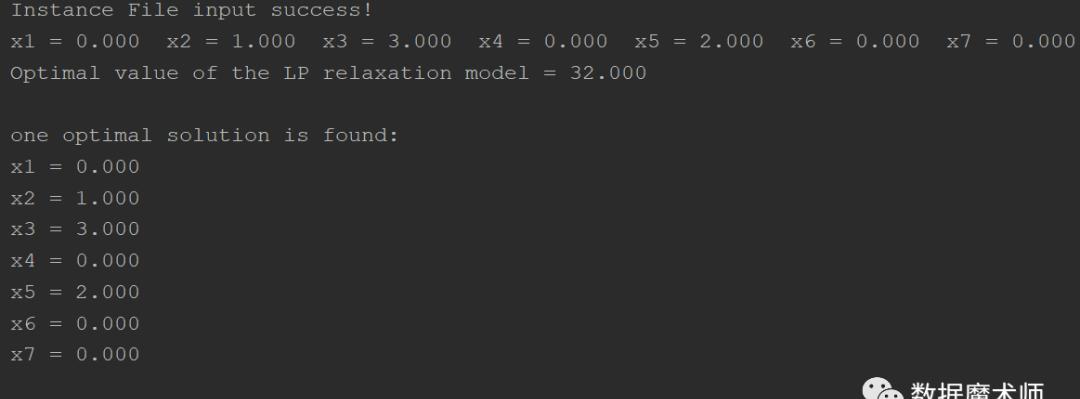
入群方式见文末!
– END –
文案&代码:周航(华中科技大学管理学院本科二年级)指导老师:秦虎老师(华中科技大学管理学院)排版:程欣悦(荆楚理工学院本科三年级)如对文中内容有疑问,欢迎交流。PS:部分资料来自网络。如有需求,可以联系:秦虎老师(华中科技大学管理学院:professor.qin@qq.com)周航(华中科技大学管理学院本科二年级:zh20010728@126.com)程欣悦 (荆楚理工学院本科三年级:1293900389@qq.com)

欢迎大家加入数据魔术师粉丝群,我们的活动将会通过粉丝群优先发布, 学习资料将通过粉丝群分享。
欲入群,请转发此文,然后扫描下方二维码联系数据魔术师小助手