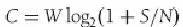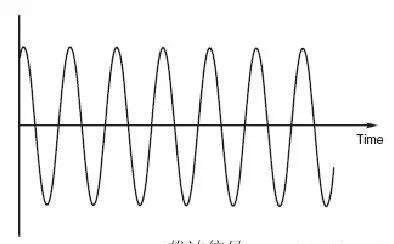
调幅调制最显而易见的的方式就是调幅了,通过调整信号幅度大小传递信息。最简单的调制是OOK(on–off keying,开关键控),载波以开关的形式传递信息。这个是数字调制的基础,并用在传递莫斯(Morse)电码上面,莫斯在早期的“无线”应用上广为采用,通过开或关的长度传递码元。在音频或其他领域应用更为常见的是,整个信号的幅度通过载波体现,如下图,这个被称为幅度调制(AM)。
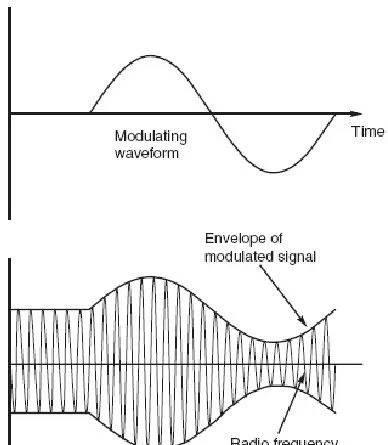
AM解调音频信号的过程十分简单,只需要一个简单的二极管包络检波电路就可以实现,如图3-3,在这个电路中二极管只允许无线信号的半波通过,一个电容被作为低通滤波器来去除信号的高频部分,只留下音频信号。这个信号直接通过放大后输出至扬声器。该解调电路十分简单和易于实现,在目前的AM收音机接收上面还在广泛采用
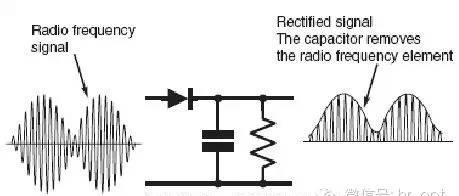
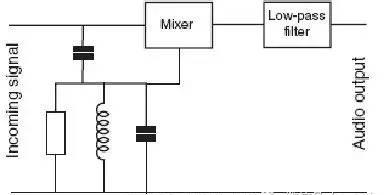
AM解调过程同样可以用更为有效的同步检波电路实现。如图3-4,射频信号被本地载波振荡信号混频。该电路的优点是比二极管检波器有更好的线性度,而且对失真和干扰的抵抗比较好。产生本振信号的方法很多,其中最简单的就是把接收到的无线信号通过高通滤波器,从而滤掉调制信号保留精确频率和相位的载波,再与无线信号混频滤波就能得到原始音频信号。
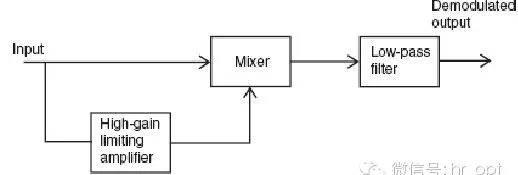
AM具备实现简单的优势,不过并不是最有效的方式,在频谱利用率和功耗方面均是如此。因此该方式在通信领域极少采用,一般只在VHF频段空中通信中采用。然而,AM在长、中、短波广播领域采用较多,因为其低成本和简单性。为了表明其低效率,我们需要看看AM操作的原理,当一个射频信号被一个音频信号调制时,波形会改变,在全调制过程中,调制后信号幅度会从零升到最高,而幅度升高到峰值时会达到载波信号幅度的两倍,这样很容易造成失真因为包络信号不能低于0。因为这种方法调制深度最大,所以叫做100%全调制。
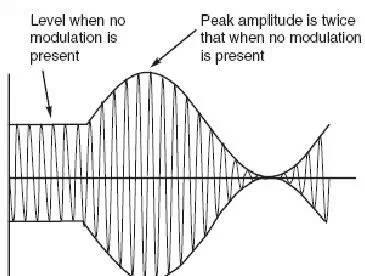
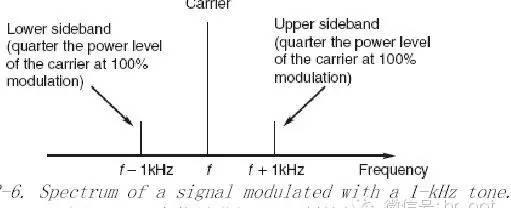
即使在全调制模式下,功耗利用率也很低。当载波被调制,频谱中两边都会产生边带,边带包含了音频信号的信息。我们可以举例阐述功耗消耗的情况,比如1kHz的语音信号在载波上进行调制,这样频谱上会在载波两边出现两个频带,如图3-6,当载波被全调制,接收的调制信号的幅度等于载波信号幅度的一半,既是功耗也等于载波信号的一半。换句话来说,边带信号的能量等于载波信号能量的一半,而每个边带只有载波能量的1/4。这样对于一个100W的发射机来说,载波能量为50W,每个边带为25W,调制过程中载波信号的功耗是恒定的,而在解调过程中需要一个载波信号。我们只需要一个边带作为有用的信号,所以总的效率等于50/150,只有三分之一的能耗得到了有效利用。
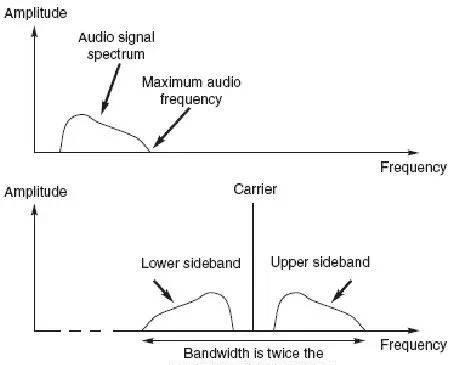
AM不仅浪费能耗,而且频谱利用率不高。如果例子中的1kHz信号被普通的音频信号取代,中频两边的频谱都会被该音频信号的频带占据,如图3-7。因此需要的频段是传输信号频段的两倍。在短波信号非常拥挤的今天,这样使非常浪费的,因此目前在该频段内的一些无线传输都采用其他更有效率的调制方法。
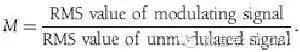
调制深度不会超过1,否则包络就会出现失真,信号会出现额外的频谱,造成干扰信号。FM调频AM是非常简单的调制方式,而通过改变频率的FM调制也一样。如下图,载波信号被调制后,频率会随着信号源电压变化。
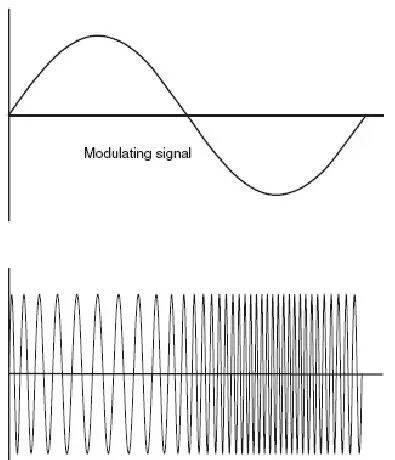
调制指数和偏离比很多情况下调制指数只是一个值并一般用于别的运算,FM调制指数指的是频率偏离相对调制频率的比例,因此会随着在载波上变化的调制偏离而改变。

然而,设计一个系统需要知道最大的调制指数,这个通过在公式中带入最大的值可以得到。

边带被调制的信号都会产生边带,在AM调制中很容易计算得到,但在FM调制中就不是那么明朗,因为这不仅于偏离相关,而且与偏离的度有关,比如说,如果调制指数为M,总的频谱通过一个复杂的公式可以得出,得到的是一个无限的离散频谱。
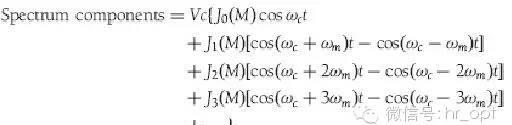
公式中,Jn(M)是第一类贝塞尔函数,ωc是载波的频率并等于2nf,ωm是调制信号的频率,Vc是载波的电平。可以看出整个频谱包括载波的频率加上载波两边的无限的边带频谱。相关的边带可以从贝塞尔函数的表格中读出,或者用计算公式得出,图3-10显示出不同的调制指数下边带的变化情况
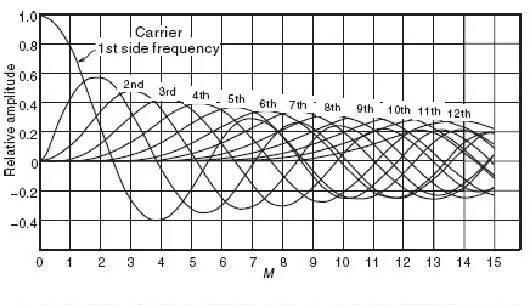
可以总结在低级别的偏离下(既窄带FM),调制信号在载波中频的两边都有边带频谱,频谱看起来跟AM信号查不多,最大的区别是较低边带超过了180°的相位。当调制指数增加,二倍中频的边带频谱就出现了(图3-11),指数继续增加,更高的边带也会出现。同时可以看到随着调制指数的升高带来边带的改变,一些频段能量升高而一些降低。
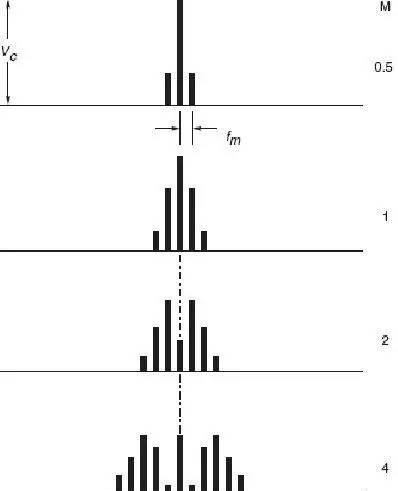
FM调制信号的频谱随着调制指数变化的情况,可以看出当指数较小时(比如M=0.5),信号频谱表现出一个载波频率和两个边带,当调制指数上升时,边带数量增多而载波频率的能量会下降。带宽很明显我们不能接受一个无限带宽的信号,所以对于低级别的调制指数只会计算头两个边带信号频谱。然而,因为调制指数的增加,更高级别边带会产生,经常需要滤波器对信号进行处理,而且这不能带来不适当的失真。为了达到要求通常需要将带宽设置为最大调制频率加上两倍偏离频率。换句话来说,在VHF FM广播中,如果采用±75 kHz的偏离,而最大调制频率为15 kHz,带宽就需要(2 × 75) 15 kHz=165 kHz,一般采用200kHz,使发射系统具备一个保护频带,且中频可以以100kHz为基础。提高信噪比已经提到FM比AM信号在宽带环境下可以提供更好的信噪比,实际上,偏离越大,信噪比越好。FM相比AM来说,提高的信噪比等于3D2其中,D是最大偏离率,在D值高的情况下非常明显。如果对音频信号进行预增强就可以更好的增加FM信号的信噪比,通常的做法是,低电平的高频音频信号会进行相比低频信号更大幅度的放大,然后再进行调制。在接收器,采用相反的处理来得到原始的音频。为了实现这个预增强,信号需要首先通过一个电容电阻(CR)网络,在截止频率点之上的频率,信号每增加8度音阶,电平就增加6dB,类似的,在接收端也进行相应的处理。频移键控许多信号系统采用频移键控(FSK)来无线传输数字信号(如下图)。图中信号频率有两种,一个代表1(mark),一个代表0(space),通过改变载波频率来传输数字信号。
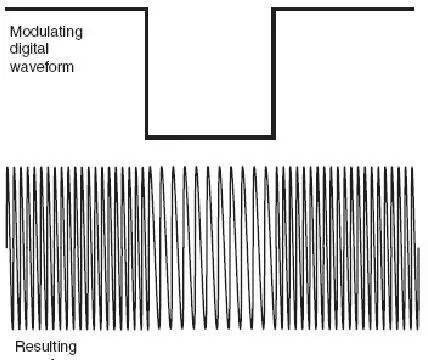
有两种方法可以用来实现用两个频率的信号传递信息。一个很明显的方法是改变载波频率,另一个是所谓的音频频移键控(AFSK),AFSK更好因为对精度有较高要求。▊相位调制调相相位调制是另一种广泛采用的调制技术,特别是在数据传输的应用中。因为相位和频率是相辅相成的(频变是相变的一种形式),两种调制方法可以用角度调制(angle modulation)来概括。为了解释调相如何工作,我们首先要对相位做出解释。一个无线信号包涵了一个正弦信号的载波,幅度从正到负程波浪形变化,一个周期后回到零点,这个同样可以由一个围绕一个零点旋转的一个点来表示,如下图所示,相位就是终点到起点的角度。
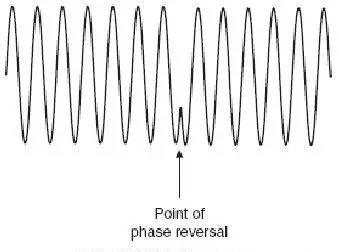
PSK 的一个问题是接收机不能精确的识别传输的信号,来判定是mark(1)还是space(0),即使发射机和接收机的时钟同步也很难实现,因为传输路径会决定接受信号的精确相位。为了克服这个问题,PSK 系统采用差分模式对载波上的数据进行编码。比如说,信号为1 的时候改变相位,信号为0 时不改变相位,在这个基础架构上可以做更多的改进,一些其它的PSK 方法也被开发了出来。一个方法是信号为1 时做90°的相移,在信号为0 时做-90°相移,这样保留了0 和1 之间180 度的相差。在简单的系统中如果不采用该方式进行传输,在传一个长序列的0 的时候有可能会失去同步,这是因为产生突发模式时相位没有改变。基于基本的PSK 会有很多改变,各个方案都有各自的优缺点,让设计人员针对具体的应用采用不同的解决方法。比如说四相相移键控(QPSK),采用了四个相位,每个相差90°,8-PSK,采用8 个相位等等。为了方便表述一个PSK 信号,我们采用相位矢量或者星座图,如图3-15。采用这个图可以很好的体现相位信息和幅度信息。在这个图里面,信号的相位用角度表示,幅度用具离圆心的距离表示。这样这个信号中的同相分量用sine 信号表示,而正交分量用cosine信号表示。大部分PSK 系统采用不变的幅度,因此圆心周围的点与圆心距离相等并只改变相对圆心的角度。对于BPSK 调相,星座图上只有两个点,其它PSK 调制可能有更多的点在圆周上。
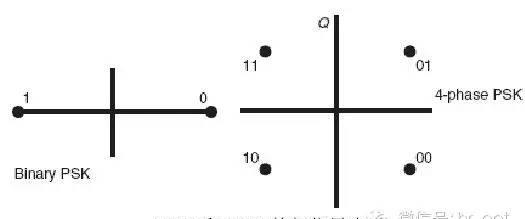
当采用测试仪器进行测试时,我们会发现在理想的星座图上的频点会出现错误。错误的原因是调制器、传输过程或者接收器会出现误差,或者系统中引入了噪声。可以想象当真实的测试比理想状态差的太多时,就会出现误码,因为解调器不能正确的判断圆周上频点的位置。使用星座图可以很快的找出错误所在,如果错误是与相位相关,星座图可以在圆环圆周再进行查找,如果错误与幅度相关,星座图可以扩大或者缩小圆环半径进行查找。采用该方法比采用其它方案查找错误有效的多。在IS-95 CDMA 无线通信系统中,从基站到手机的前向链路采用了QPSK 调制,并采用绝对相位来表述模型。QPSK 有四个相位点,当从一种状态跳向另一种时,可能会产生过零点的相位跳变。在从手机到基站的反向链路中,偏移四相相移键控(offset-QPSK,O-QPSK)被采用,这样可以避免QPSK 造成的180°相位跳变。考虑到星座图上X、Y 分量上的相反的向量,一般来说,两种分量是同时产生的,这样就会造成过零点相位跳变。在O-QPSK 中一个分量被延时了,所以就避免了向量直接过零点,从而简化了无线设计。最小相移键控因为双相相移键控会在“1”和“0”之间出现激烈的跳变,这样在频谱上会造成非常长的边带滚降,这在许多应用是很不理想的。我们可以采用滤波器滤除部分频带,滤的越多带宽虽然变窄了,但1 和0 的分界会变得模糊。为了克服这个问题,另一种调制手段——称作高斯最小频移键控(GMSK)被广泛采用了,最为大家所知的就是用在了GSM 无线通信标准中。GMSK 起源于另一个调制方法最小相移键控(MSK),该方法也具有连续的频谱,因为是在载波的过零点处产生频变,所以相位改变是非离散的。下图表述了MSK 的调制,可以看到并没有相位的突变,这个MSK 表示出的“1”和“0”的区别主要是体现在载波频率被“0”调制时是“1”的两倍,从调制指数来说的话就是M=0.5。
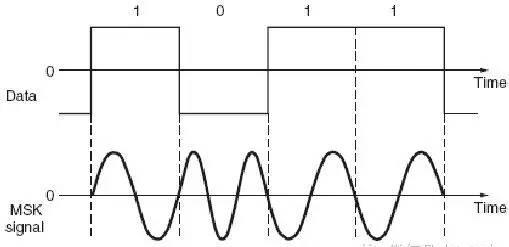
这个主意看起来很好,而实际上在MSK 调制系统中信号出来后带宽很大,最大带宽已经达到了数据率的带宽。MSK 的信号频谱显示其边带很长,甚至超过了传输的数据率(下图)。如果通过一个低通滤波器对调制信号进行滤波,可以使其适应载波。对滤波器的要求是必须具备陡峭的频率截止和窄的通带,其冲击响应(IR)不应overshoot,一个理想的滤波器就是高斯滤波器,对冲击响应呈现出高斯函数。
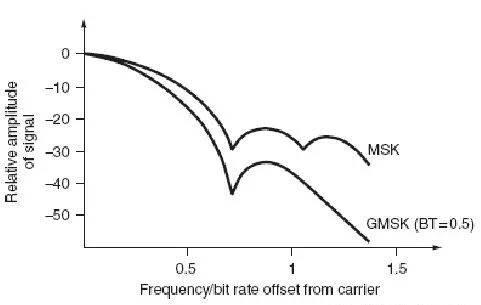
有两种方式实现GMSK,最明显的一种方法是让信号通过高斯滤波器然后再在一个调制指数为0.5 的调频电路进行调制,如图3-18。同时该方案的缺点是调制指数必须是精确的0.5,实际情况是,由于元器件的公差和漂移这个方案并不合适。
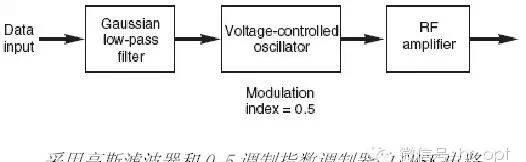
第二个方式被广泛的应用,就是所谓的正交调制。“正交”的意思是一个信号的相位相对另一个是正交(相差90°)的,即一个同相信号一个是正交信号,也就是通常说的I-Q调制(下图)。当采用该方法进行调制时,调制指数可以非常精确的达到0.5 而无需额外的设置和调整,所以实现起来就比较容易。在接收器解调部分,可反向执行该电路。
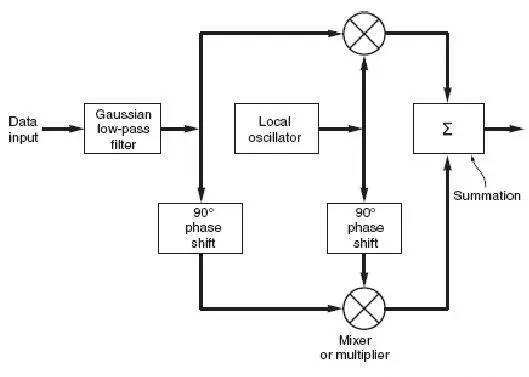
GMSK 的另一个好处是可以采用非线性放大器而不会产生失真,因为调制后信号幅度的变化不会带有任何有用的信息,因此该方案相对别的一些调制方式也更加能抗噪声。正交幅度调制另一个广泛应用的数据传输方法是所谓的正交幅度调制(QAM)。该信号中两个载波相位相差90°,被调制后输出信号在幅度和相位都有改变。因此不管幅度还是相位都会进行变化,所以被看成是混合幅度和相位的调制。3bit 的数据可以分为一组并用表格中的幅度和相位组合来表示。
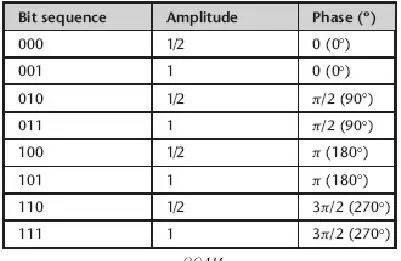

使用正交编码,在一个频带中可以传输更大量的数据。实现方法是,数据与码片(chip)相乘(如下图),码片是不断送出的指定的编码信号,每个数据位都要与码片的每个位相乘。因此可以看出扩频比就是一个码片中的比特位数。
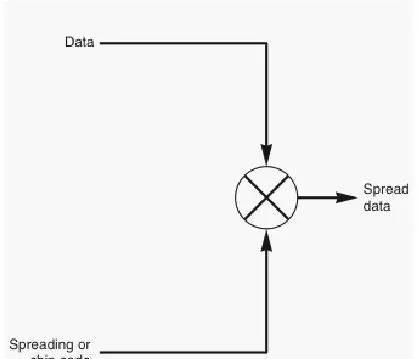
为了产生这个能携带多个信息的单载波信号,每个扩频后的信号会进行相加得到一个输出信号(下图),然后再调制和上变频后在天线端传输出去。
在接收端采用相反的步骤,信号被下变频至基带信号。这里该信号会与相关的码片相乘,得到的结果会根据码片数进行相加,即所谓的相干解扩。通过与不同的码片相乘,不同的原始信息就会被萃取出来。为了表示系统是如何工作的,我们用下图来表示。我们假设扩频比为4,在3-22 中,可以看到a 和b 是扩频码(实线部分为一个码片),扩频码a 与信息c 相乘得到扩频后的数据d,而扩频码b 与信息e 相乘得到扩频后的数据f。而扩频后的d 和f 进行相加运算得到基带信号g,然后再在载波上进行调制和无线传输。
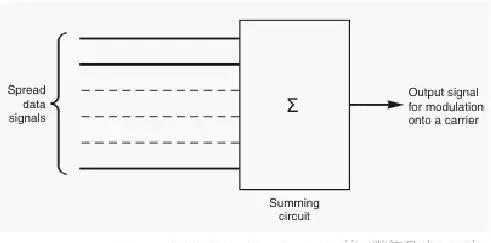
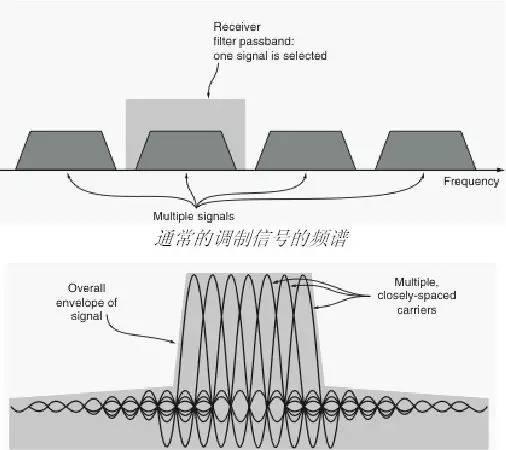
接收机在这种情况下,码片a(既是h 的波形)再与基带信号g 相乘就可以得到i,因为扩频比为4,每组4 个比特相加,就可以生成与c 相同的j 信号完成解扩。当一个伪随机序列扩频码被使用后,需要执行相关的处理。伪随机扩频编码得到使用,而不是正交码,这时发射机和接收机需要产生同样的伪随机码,通过让接收机和发射机采用相同的算法产生序列可以方便的实现。采用伪随机码的缺点是编码不会正交,因此重新产生正交信号时会出现一些误码。正交频分复用另一种广泛应用的调制方法是正交频分复用(OFDM),编码正交频分复用(COFDM)是其中的一种形式,COFDM 多用在Wi-Fi 应用里面,比如IEEE 802.11,包括DAB 也采用该方法,另外4G 无线通信标准中也将采用该调制方法来提高数据率。一个COFDM 信号一般包含了一系列间隙很窄的调制载波。通常对语音、数据或其他信号进行调制时,边带会在两边扩展,接收机必须接收到整个频段的信号来执行解调,因此,当信号传输到接收机时,各个频道之间必须有间隔,这样接收机才能用滤波器将它们分开。而COFDM 不需要这样的条件,尽管各个载波的边带会有混叠现象,但也可以无干扰的接收到,因为各个载波之间是相互正交的,这个可以通过将载波的间隔与符号周期的倒数相等来实现。下图1表示了传统的无线接收机接收到的频谱状况,而下图2表示了一个COFDM 信号频谱。
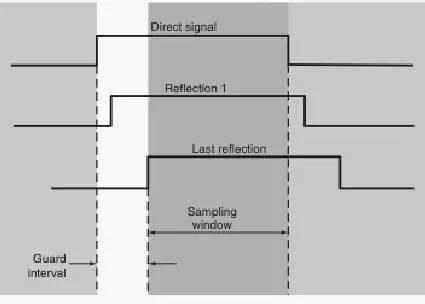
为了解释这是如何工作的,我们必须看一看接收机,接收机可以看成一个解调器的集合,一个解调器把对应载波的信号转换成DC 信号,相应的符号周期上集成的信号从载波上重建,其他解调器再解调其他的载波。因为载波间隙与符号周期的倒数相同,因此整个符号周期内组成了一个圆,它们的和加起来为0,换句话来说,就不会有干扰了。发射和接收系统的一个要求是必须是线性的,因为非线性会在载波之间造成互调干扰,会并带来意想不到的信号干扰和削弱正交信号。COFDM 多载波的高功率峰均比(peak-to-average)需要发射机的末端RF 放大器在平均功率很低的情况下处理高的峰值功率,这样会使系统效率变低。在一些系统中,峰值受到了限制,尽管会带来高的误码率对系统产生失真,但可以引入纠错(EC)算法来克服。待传输的数据会先根据载波进行扩展,每个载波会携带一部分数据,这样就降低了每个载波携带的数据率。低数据率的好处是受到的干扰会大大降低。通过增加一个保护时间(或保护间隔),如下图,可以在信号稳定后再进行处理,在这个时间内不会有新的信号传进来改变时序和相位。
在多个载波上分配数据还有一些好处。多径效应的干扰只会在少部分载波上产生,而大部分会被正确的接收。使用纠错编码技术,意味着增加了信号携带的数据,但可以让接收机正确重建几乎所有的数据。这样能实现是因为纠错编码是在信号的不同部分传输,这个纠错编码可以说是编码正交频分复用的“编码”。带宽和容量通信系统的一个重要的考量是系统的数据吞吐量。因为用户对数据量和速度的要求是无止境的,我们必须合理利用每一个频段。可以看到有多种调制手段可以用到,它们中的一些在某些场合比其他的更为高效。然而,有一些定律左右着能传输的信息量。信道的带宽是决定信号携带数据量的主要因素。带宽从字面上来说是指该信道用Hz 单位度量的频道的宽度,可以用高的频率减去低的频率轻松的得到。奈奎斯特采样定律定义要恢复频率带宽为W 的信号,必须采用超过2W 带宽的载波进行采样。该转换也可以看成:有一个带宽为W 的信号,假设该信号不经过模数转换变成二进制编码时最高的频率为2W,但如果要进行模数转换,采样的数据率(bps)要是原始模拟信号带宽的两倍。传输多级信号必须大大增加带宽容量。传输多级信号的问题是必须把每个信号从外部干扰—特别是噪声–中分辨出来。香农定律就描述了这种情况的发生,该定律是由Claude Shannon 定义,是现代计算科学形成的基础,而且是信息学中关于一个数据信道中能获得的最大数据率传输的表述。香农定律定义了在一个信道中能传输的最大无损失数据率是与带宽和信噪比相关的,该公式表述如下: