逻辑回归（Logistic Regression）在20世纪早期的生物科学得到应用，广泛应用与很多社会科学，很多事物发展的规律符合逻辑回归曲线。
本文介绍的逻辑回归应用于分类任务，即目标变量是分类变量。
比如：
预测邮件是否是垃圾邮件（1）或（0）
预测肿瘤是否是恶性肿瘤（1）或（0）
其中1和0分别表示是和否。
考虑这样一个常见，我们需要对电子邮件是否属于垃圾邮件进行分类。如果我们对这类问题使用线性回归，就需要设置一个阈值，根据这个阈值可以进行分类。假设实际类为恶性，预测连续值为0.4，阈值为0.5，则该数据点被归为非恶性肿瘤，这种模型会导致严重的后果。
从这个例子可以看出，线性回归不适合分类问题，线性回归是无界限的，因此引入了逻辑回归，逻辑回归的界限值为0到1。
1.逻辑回归模型
输出 ：0 或 1
模型的假设函数：
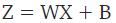
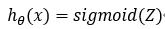
其中Sigmoid函数为：
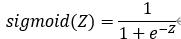
用图形表示：
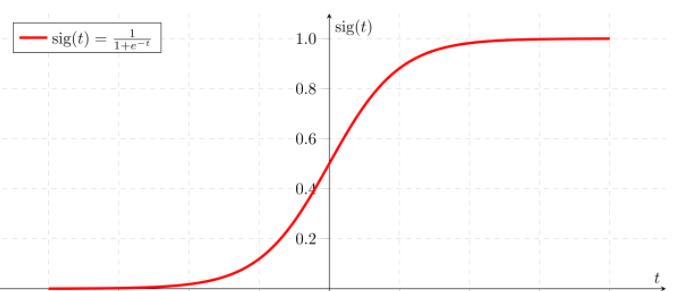
由公式可知，如果变量 Z 趋向于无穷大，那么预测变量 Y 等于1；如果变量 Z 趋向于负无穷大，预测变量 Y 等于0。
2.模型的假设函数分析
假设函数输出变量的含义是预测概率，用来推断在给定输入值X时，预测值与真实值的置信度。
考虑如下例子，预测邮件是否是垃圾邮件，给定如下输入变量：
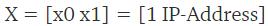
基于输入变量 x1 的值，假设我们得到的估计概率是0.8，也就是说属于垃圾邮件的概率是0.8。
数学上可以写成：
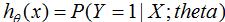
含义为：模型参数为，给定输入变量X，输出变量Y等于1的概率。
对于二分类模型来说，由上式可以推导如下等式：
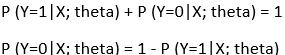
这就证明了“逻辑回归”这个名称的合理性。首先将数据拟合到线性回归模型中，然后通过逻辑函数预测目标标量。
3.逻辑回归类型
1. 二元逻辑回归
目标变量只有两个可能的结果，例如：是否是垃圾邮件
2. 无序多项逻辑回归
目标变量是三个或三个以上的类别，与顺序无关，例如：预测哪种食物更受欢迎（素食，非素食，纯素食）
3. 有序多项逻辑回归
目标变量是三个或三个以上的类别，与顺序有关，例如：预测电影评分，从1颗星到5颗星。
4.决策边界
为了预测数据属于哪一类，可以设置一个阈值，比较预测的估计概率和阈值，得到分类结果。
逻辑回归的阈值常常设置为0.5，也就是说，如果预测的估计概率≥ 0.5时，则属于垃圾邮件，反之则不属于垃圾邮件。
决策边界可以是线性的也可以是非线性，多项式阶数的增加可以得到复杂的决策边界，我们可以用支持向量机的核函数来理解。
5.损失函数
逻辑回归的损失函数为：
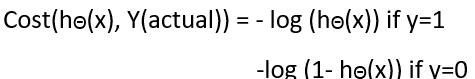
线性回归使用均方误差作为其损失函数，为什么逻辑回归不使用均方差？
因为若使用均方误差作为逻辑回归的损失函数，那么该函数是非凸函数。若损失函数是非凸函数（Non-convex）时，梯度下降算法可能收敛局部极小值；损失函数是凸函数（Convex）时，梯度下降算法收据全局最小值。如下图：
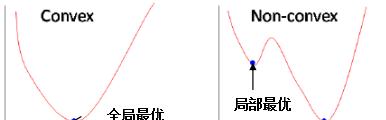
损失函数详细解释
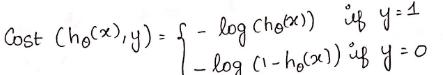
如果真实目标变量等于1，即：
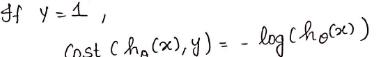
对应的图形如下：
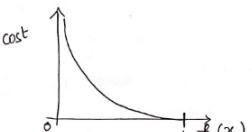
如果真实目标变量等于0，即：
对应的图形如下：
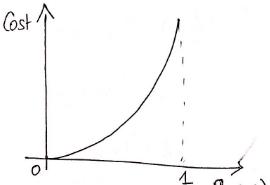
结合上面的介绍，逻辑回归损失函数简化为：
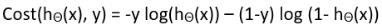
如果y=1时，损失函数为：
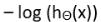
如果y=0时，损失函数为：
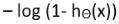
6.为什么使用这个损失函数
我们假设
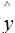是给定输入变量 x ，输出变量 y 为1的概率，即：
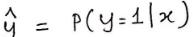
那么输出变量y为0的概率：
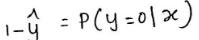
根据上面两式，可得模型输出变量y的概率为：
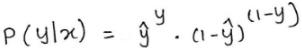
上式是不是有点眼熟，其实上式就是似然函数的定义。
我们对上式取对数，得：
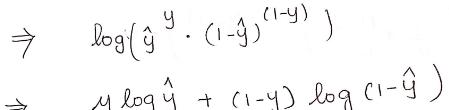
这个式子和我们前面介绍过的损失函数是相反数，即：
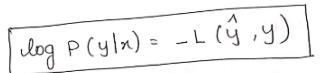
因此，逻辑回归最大化似然函数等价于最小化损失函数，这就是我们为什么使用这个损失函数的原因。
7.逻辑回归模型的求解过程
我们使用梯度下降法求解模型的最优参数：
上图知道了不同变量的梯度表达式，因此损失函数的参数梯度为：
逻辑回归模型的Python实现：
def weightInitialization(n_features): w = np.zeros((1,n_features)) b = 0 return w,bdef sigmoid_activation(result): final_result = 1/(1 np.exp(-result)) return final_resultdef model_optimize(w, b, X, Y): m = X.shape[0] #Prediction final_result = sigmoid_activation(np.dot(w,X.T) b) Y_T = Y.T cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) ((1-Y_T)*(np.log(1-final_result))))) # #Gradient calculation dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T)) db = (1/m)*(np.sum(final_result-Y.T)) grads = {“dw”: dw, “db”: db} return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations): costs = [] for i in range(no_iterations): # grads, cost = model_optimize(w,b,X,Y) # dw = grads[“dw”] db = grads[“db”] #weight update w = w – (learning_rate * (dw.T)) b = b – (learning_rate * db) # if (i % 100 == 0): costs.append(cost) #print(“Cost after %i iteration is %f” %(i, cost)) #final parameters coeff = {“w”: w, “b”: b} gradient = {“dw”: dw, “db”: db} return coeff, gradient, costsdef predict(final_pred, m): y_pred = np.zeros((1,m)) for i in range(final_pred.shape[1]): if final_pred[0][i] > 0.5: y_pred[0][i] = 1 return y_pred
损失函数与迭代次数的关系：
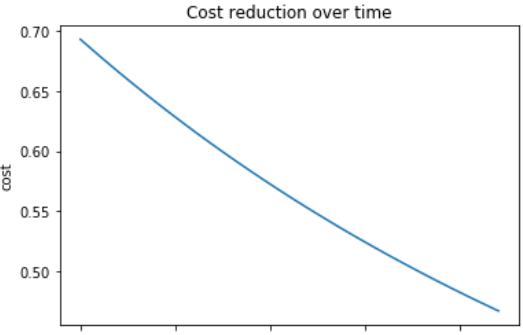
此Python实现是用于二元逻辑回归，对于超过两个类的数据，我们建议使用softmax回归。
