部编版语文1至6年级下册课文朗读与图文讲解部编版语文1-6年级下册单元及期中期末测试卷(可下载)部编版语文1至6年级下册各单元知识点归纳人教版数学1至6年级下册各单元知识点复习人教版数学1至6年级下册单元及期中期末测试卷(可下载)北师大版小学数学1-6年级下册期末测试卷(可下载)苏教版数学1-6年级下册期末测试(可下载)人教版数学下册期末复习资料与考试试卷综合整理人教PEP版3至6年级英语下册单元及期中期末测试卷部编版语文1至6年级下册期末复习资料与测试卷综合整理
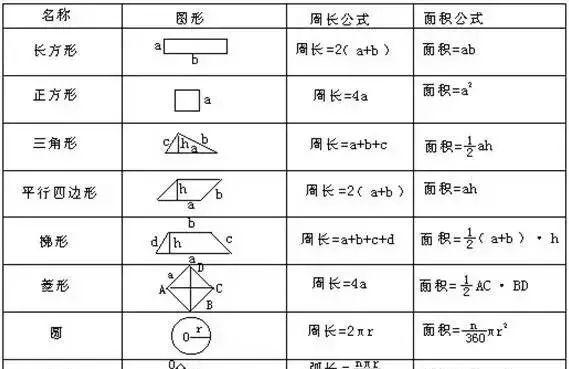
我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形,面积及周长都有相应的公式直接计算,如下表:
实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下
例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
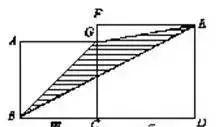
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.
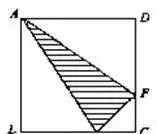
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.
解:
S△ABE=S△ADF=S四边形AECF=12
在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,
∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。如右图那样重合.求重合部分(阴影部分)的面积。
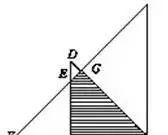
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形
总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:
一、相加法
这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.
例如:求下图整个图形的面积
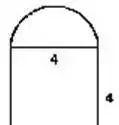
一句话:半圆的面积 正方形的面积=总面积
二、相减法
这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.
例如:下图,求阴影部分的面积。
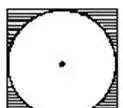
一句话:先求出正方形面积再减去里面圆的面积即可.
三、直接求法
这种方法是根据已知条件,从整体出发直接求出不规则图形面积.
例如:下图,求阴影部分的面积。
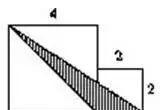
一句话:通过分析发现阴影部分就是一个底是2、高是4的三角形
四、重新组合法
这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.
例如:下图,求阴影部分的面积。
一句话:拆开图形,使阴影部分分布在正方形的4个角处,如下图。
五、辅助线法
这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可
例如:下图,求两个正方形中阴影部分的面积。
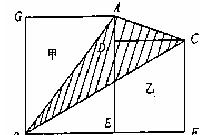
一句话:此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便(如下图)
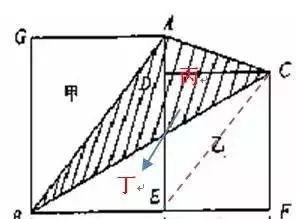
根据梯形两侧三角形面积相等原理(蝴蝶定理),可用三角形丁的面积替换丙的面积,组成一个大三角ABE,这样整个阴影部分面积恰是大正方形面积的一半.
六、割补法法
这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.
例如:下图,若求阴影部分的面积。
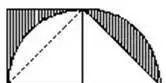
一句话:把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.
七、平移法
这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.
例如:下图,求阴影部分的面积。

一句话:可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法
这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.
例如:下图(1),求阴影部分的面积。
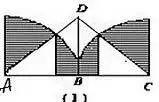
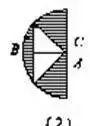
一句话:左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.
九、对称添补法
这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.
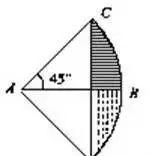
例如:下图,求阴影部分的面积。
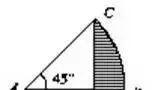
一句话:沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
十、重叠法
这种方法是将所求的图形看成是两个或两个以上图形的重叠部分。
例如:下图,求阴影部分的面积。
一句话:可先求两个扇形面积的和,减去正方形面积,因为阴影部分的面积恰好是两个扇形重叠的部分.
经典例题
一、有简便计算的
任意一个正方形与它内切圆的面积之比都是一个固定值,即:4∶π(圆面积是正方形面积的78.5%)
1.如图,求阴影部分的面积.(单位:厘米)
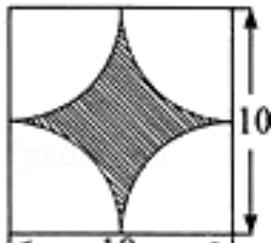
方法:正方形面积-半径为5厘米的圆的面积=阴影面积
提示:圆的半径=正方形边长的一半
2.计算如图阴影部分的面积.(单位:厘米)
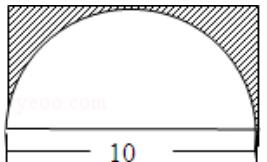
方法:长方形面积-直径为10的半圆面积=阴影面积
提示:长方形的长=圆的直径,宽=圆的半径
3.求出如图阴影部分的面积:单位:厘米.
方法:长方形面积-半径为4的半圆面积=阴影面积
提示:长方形的长=圆的直径,宽=圆的半径
4、
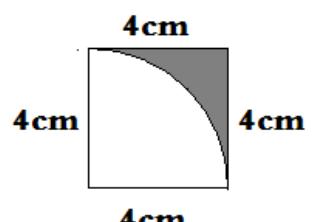
方法:正方形面积-半径为4的扇形面积=阴影面积
提示:正方形的边长=扇形的半径
5、
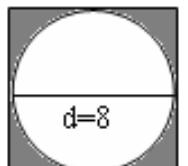
方法:正方形面积-直径为8的圆面积=阴影面积
提示:正方形的边长=圆的直径
6、
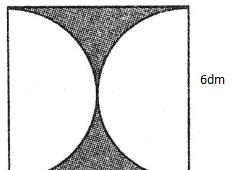
方法:正方形面积-直径为6的圆面积=阴影面积
提示:正方形的边长=圆的直径
7、
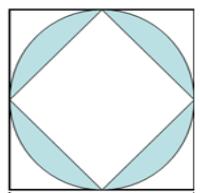
方法:圆的面积-内正方形的面积=阴影面积
提示:
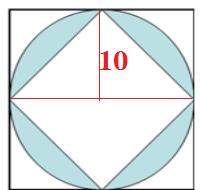
圆的直径=外正方形的连长20
内内正方形分为两个两样的三角形
三角形的底=圆的直径20,高=圆的半径10。
二、割补平移的
1、
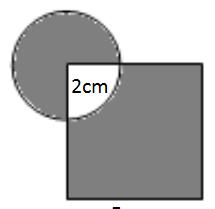
方法:将组合图形拆分
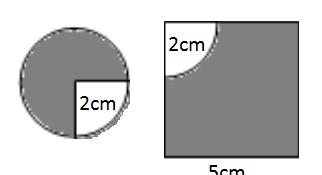
圆形面积 正方形面积-半圆的面积=阴影面积
提示:也可以这样计算:
正方形面积 圆面积的四分之三=阴影部分面积
2、
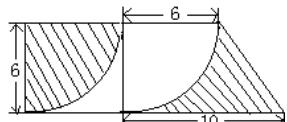
提示:此图相当于计算上底是6,下底是10,高是6的梯形面积。
3、
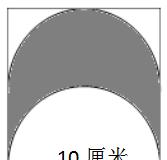
提示:此图相当于计算长是10,宽是5的长方形面积。

4、
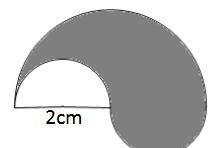
提示:此图相当于计算半径为2的半圆面积。
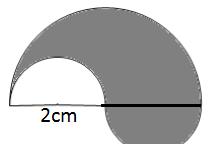
5、
提示:此图计算上底是5下底是13,高是5的梯形面积,再减去底是5,高是5的三角形面积。
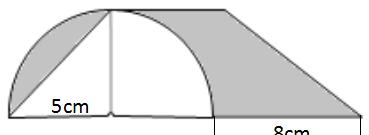
6、
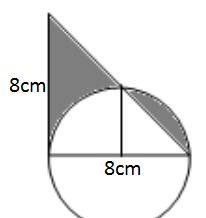
提示:计算底是8,高8的三角形面积,减去底是8,高是4的三角形的面积。
7、
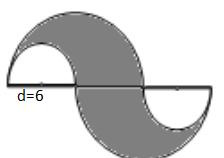
提示:计算半径是6的大圆的面积,再减去直径是6(半径是6÷3)的小圆面积。可用圆环公式计算:3.14×(外圆半径的平方-内圆半径的平方)
三、方程法
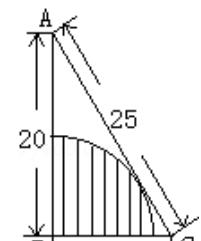
1.计算如图中阴影部分的面积.单位:厘米.
2、如图所示,圆的周长12.56厘米,圆的面积与长方形的面积相等。求图中阴影部分的面积。
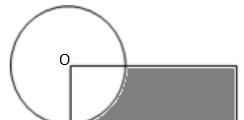
提示:阴影部分相当于圆面积的四分之三。
根据圆的周长计算出圆的半径,计算出圆的半径和面积;然后圆的面积乘四分之三。
四、自己测量
量出你需要的数据,列式计算阴影部分的面积。(4分)(测量结果取整厘米)

提示:
半圆的直径相当于梯形的上底。
梯形的面积减去半圆的面积=阴影部分面积。
五、一般的
1.求下图阴影部分的面积.(单位:厘米)
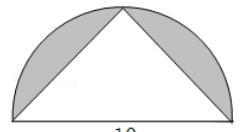
提示:半圆面积-半圆的面积=阴影部分面积
2.求阴影部分图形的面积.(单位:厘米)
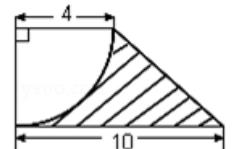
提示:梯形的面积-圆面积的四分之一=阴影部分面积