初一数学??上册内容
下个月我们就将迎来这学期第一次大考“期中考试”，月考和期中考的时间离的很近，复习的时间也很少，所以同学们要抓紧了。不想落后他人，知识点抓紧预习复习起来。今天，王老师和大家分享的是初一数学上册【期中复习】之有理数，相关题型 考查形式 易错点！
有理数相关题型：排序，给几个不同形式的有理数和无理数，进行比较大小然后排序考查形式：选择题易错点：正确区分有理数和无理数，小数不一定是无理数，2/3这样的数是有理数。知识点1：有理数的有关概念有理数：整数和分数统称为有理数。注：(1)有时为了研究的需要，整数也可以看作是分母为1的数，这时的分数包括整数。但是本讲中的分数不包括分母是1的分数。
(2)因为分数与有限小数和无限循环小数可以互化，上述小数都可以用分数来表示，所以我们把有限小数和无限循环小数都看作分数。(3)“0”即不是正数，也不是负数，但“0”是整数。整数包括正整数、零、负整数。例如：1、2、3、0、－1、－2、－3等等。分数包括正分数和负分数，例如：1/2、0.6、－1/2、－0.6等等。知识点2：有理数的分类(1)按整数、分数的关系分类：
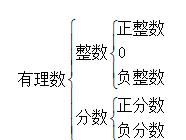(2)按正数、负数与0的关系分类：
注：通常把正数和0统称为非负数，负数和0统称为非正数，正整数和0称为非负整数（也叫做自然数），负整数和0统称为非正整数。如果用字母表示数，则a>0表明a是正数；a<0表明a是负数；a≥0表明a是非负数；a≤0表明a是非正数。知识点3：数轴数轴是理解有理数概念与运算的重要工具，数与表示数的图形（如数轴）相结合的思想是学习数学的重要思想。正如华罗庚教授诗云：数与形，本是相倚依，焉能分作两边飞。数缺形时少直觉，形少数是难入微。数形结合百般好，隔裂分家万事非。切莫忘，几何代数统一体，永远联系，切莫分离！数与形的第一次联姻——数轴，使数与直线上的点之间建立了对应关系，揭示了数与形的内在联系，并由此成为数形结合的基础。1.数轴的定义：规定了原点、正方向和单位长度的直线叫做数轴。数轴的定义包含三层含义：(1)数轴是一条直线，可以向两端无限延伸；(2)数轴有三要素——原点、正方向、单位长度，三者缺一不可；(3)原点的选定、正方向的取向、单位长度大小的确定，都是根据实际需要“规定”的（通常取向右为正方向）。2.数轴的画法：(1)画一条直线（一般画成水平的直线）。(2)在直线上选取一点为原点，并用这点表示零（在原点下面标上“0”）。(3)确定正方向（一般规定向右为正），用箭头表示出来。(4)选取适当的长度作为单位长度，从原点向右，每隔一个单位长度取一点，依次表示为1，2，3……；从原点向左，每隔一个单位长度取一点，依次表示为－1，－2，－3……
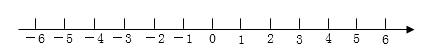注：(1)原点的位置、单位长度的大小可根据实际情况适当选取；(2)确定单位长度时，根据实际情况，有时也可以每隔两个(或更多的)单位长度取一点，从原点向右，依次表示为2，4，6，……；从原点向左，依次表示为－2，－4，－6，……；3.数轴上的点与有理数的关系：所有的有理数都可以用数轴上的点表示。正有理数可以用原点右边的点表示，负有理数可以用原点左边的点表示，零用原点表示。4.利用数轴比较有理数的大小：在数轴上表示的两个数，右边的数总比左边的数大。正数都大于0；负数都小于0；正数大于一切负数。知识点4：相反数1.相反数的定义：(1)相反数的几何定义：在数轴上原点的两旁，到原点距离相等的两个点所表示的数，叫做互为相反数。如，4与－4互为相反数。(2)相反数的代数定义：只有符号不同的两个数（除了符号不同以外完全相同），我们说其中一个是另一个的相反数。2.相反数的性质：任何一个数都有相反数，而且只有一个。正数的相反数是负数，负数的相反数是正数，0的相反数是0。0是唯一一个相反数等于本身的数。反之，如果a=-a，那么a一定是0。3.相反数的特征：若a与b互为相反数，则a b=0（或a=-b）若a b=0（或a=-b），则a与b互为相反数。4.求一个数的相反数的方法：（见书）5.多重符号的化简：(1)在一个数的前面添上一个“＋”号，仍然与原数相同，如＋5＝5，＋（－5）＝－5。(2)在一个数的前面添上一个“－”号，就成为原数的相反数。如－（－3）就是－3的相反数，因此，－（－3）＝3。知识点5：绝对值的概念1.绝对值的几何定义：一个数a的绝对值就是数轴上表示数a的点与原点的距离，数a的绝对值记作“丨a丨”2.绝对值的代数定义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0。
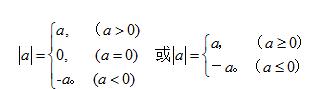知识点6：有理数大小的比较正数都大于0，负数都小于0，正数大于一切负数，两个负数，绝对值大的反而小。利用数轴，在数轴右边的数永远大于左边的数。
