(一)求函数定义域
1、函数定义域是函数自变量的取值的集合,一般要求用集合或区间来表示;
2、常见题型是由解析式求定义域,此时要认清自变量,其次要考查自变量所在位置,位置决定了自变量的范围,最后将求定义域问题化归为解不等式组的问题;
3、如前所述,实际问题中的函数定义域除了受解析式限制外,还受实际意义限制,如时间变量一般取非负数,等等;
4、对复合函数y=f[g(x)]的定义域的求解,应先由y=f(u)求出u的范围,即g(x)的范围,再从中解出x的范围I1;再由g(x)求出y=g(x)的定义域I2,I1和I2的交集即为复合函数的定义域;
5、分段函数的定义域是各个区间的并集;
6、含有参数的函数的定义域的求解需要对参数进行分类讨论,若参数在不同的范围内定义域不一样,则在叙述结论时分别说明;
7、求定义域时有时需要对自变量进行分类讨论,但在叙述结论时需要对分类后求得的各个集合求并集,作为该函数的定义域;
(二)求函数的值域
1、函数的值域即为函数值的集合,一般由定义域和对应法则确定,常用集合或区间来表示;
2、在函数f:A→B中,集合B未必就是该函数的值域,若记该函数的值域为C,则C是B的子集;若C=B,那么该函数作为映射我们称为“满射”;
3、分段函数的值域是各个区间上值域的并集;
4、对含参数的函数的值域,求解时须对参数进行分类讨论;叙述结论时要就参数的不同范围分别进行叙述;
5、若对自变量进行分类讨论求值域,应对分类后所求的值域求并集;
6、求函数值域的方法十分丰富,应注意总结


三、典例解析
1、定义域问题








2、求值域问题

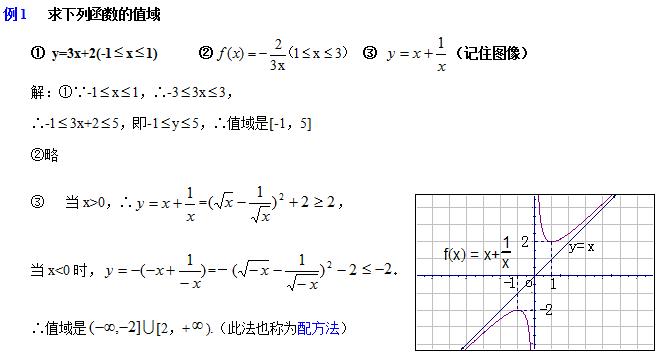





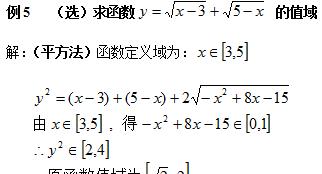
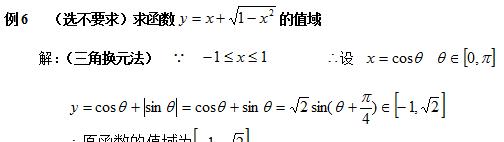
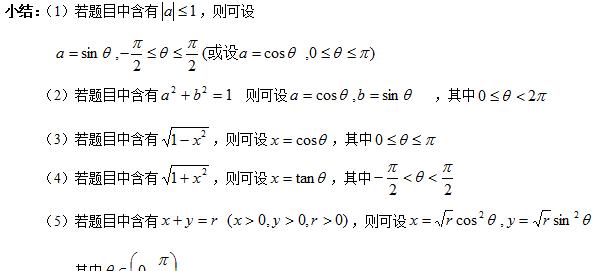
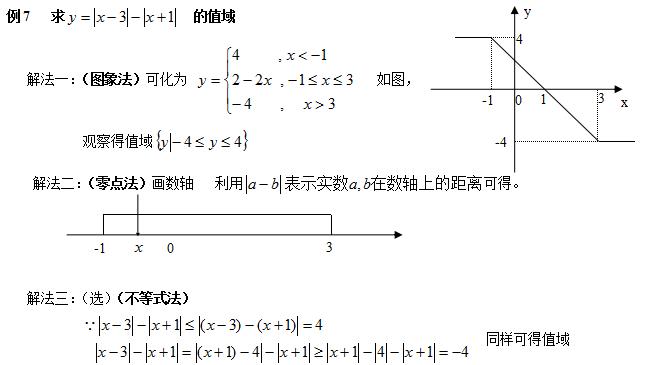








练习:



名校谈新高考引领下的高中教学和备考
常用函数与图象
重要的十类函数图象
高三数学一轮专题课——函数图象和性质复习研究
高中数学函数全面优质讲义,近乎完美的总结,不容错过!
例谈函数中容易混淆的问题