上一期我们简单聊了一下虚数概念的提出,i在数学上的意义,比如,它让任何的二次方程都有了根,当然这只是最简单的一个小方面。但有人说,求解方程的根,其实本质上还是在解决数学自身的问题,虚数没有对应任何的物理实在。还有人说,虚数揭示了深刻的宇宙意义,它是由现实通向虚空的大门。这是真的吗?虚数究竟是不是真实存在的?
1、虚数究竟真实存在吗?
让多数人对虚数感到困惑事实有一部分原因是“虚数”这个名字本身所导致的。“虚数”听上去好像就是一个虚无缥缈并不存在的数。
但高斯本人也觉得这个名字起得极差。他并不喜欢使用imaginary number(虚数)来称呼虚数,因为这个单词意为:想象中的;虚构的。他其实更倾向使用lateralnumber(“侧数”或者“旁数”)来称呼虚数。他这样做似乎在暗示虚数并不是无中生有,它就在你所熟悉的数轴的旁边。
认为虚数很“虚”的另一原因似乎是,在生活中人们好像的确用不到虚数。比如,我们描述今天吃了几个苹果?今天的最高的温度,世界冠军的奔跑速度,我们都用不到虚数。而且它与我们的感官不相符,复数可以像向量那样有方向,这就与人们印象中规规矩矩的数字不大一样。所以有人认为,在某些特定的物理场合,我们使用虚数,那是因为虚数被用作某种技巧进行使用,尽管引用虚数很方便,但归根到底这只是一种可有可无的数学工具罢了。
但是,回到这个问题本身来看。我们会发现这个问法本身存在一个问题——什么是真实存在?

这个很难去说,每个人的理解角度也不同。比如说,不用说对虚数了,我们就说负数,你就很难说它存在或者不存在,当你说“我有-1个苹果”,那么这个-1在现实生活中其实是毫无意义的,现实中我们看不见也摸不着的这-1个苹果,但是你也能接受-1这个数的概念的存在,没有觉得-1这个数字它是不存在的,或者对它的存在性质疑。
所以,对于这个问题,如果一定要回答的话。那我们就必须要回到找x^2 1=y方程解的过程。我们说,在实数轴上找不到解,但在复平面上却可以找到函数的解,只不过,这两个解落在了实数轴以外。这个拓展出来的虚轴,是一个新的维度,我们只能说虚数存在在了一个拓展出的维度中,一个看似抽象但是可以被我们想象到的维度中。但是这个所谓的“新的维度”的说法,也只是受限于人类自身的认知,我们不能说我们对数的认识是不带有偏见的。你如何以为数就一定得在一维轴上?二维复平面就一定是人们想象出的?如果我们能打破这些刻板的思维,尤其是习惯用复平面思考问题后,我们可能就会对复数的实在性有一个新的认识。
2、复数有哪些用途?
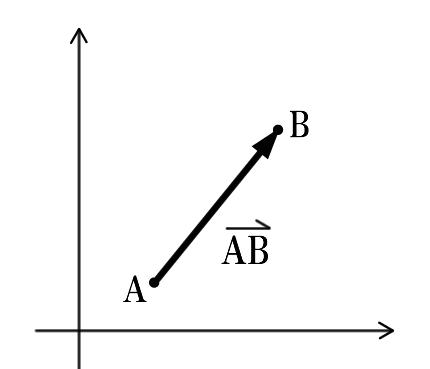
复数的一个很重要的属性,就是可以将其看成向量,这样一来,复数就能表示平移,旋转,镜像以及伸缩,这些功能显然是实数完全无法做到的。在几何意义上,数已经可以闭着眼在复平面上旋转跳跃了。比如说我们给定一个数5,我们在5的基础之上,给他乘上一个i的平方,那么这意味着什么呢?5变成5i^2其实就-5,这就是一个旋转的过程,5绕着零点逆时针转了180°。
正是因为这样的特质,复数在描述某种方向变化或周期性改变的物理变化的时候,有着明显的优势。这主要表现在,几何图形处理、波函数拟合、交流电分析等诸多方面,这也意味着与此相关的物理、工程领域有了属于他们的数学语言,比如:电路分析,电气工程、信号分析,量子力学等等:
因为无论是电路还是各类信号。从本质上来说,都是电磁波,大家可以想象一下你所理解的那种最直观的波,比如水波、机械波这样的一个具有s曲线样的波,对这样的物理形态,我们要怎么样去用一个数学模型去描述他呢?
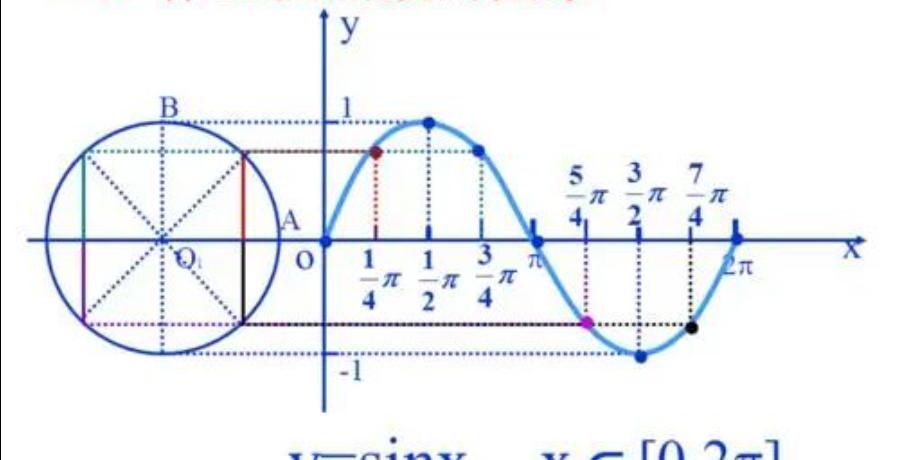
最初,人们用数学三角函数来表示这样的一个形式。以正弦函数(直角三角形里的对边比斜边的比值)为例,它的样子就是一个波浪,并且具有周期性,每经过360度(2π),它的函数值就重复一遍。
那有人就会问了,那三角函数来表示波不是很好吗?为什么又要引进到复平面里面来表示呢?
这就跟欧拉公式有一定的关联,欧拉公式的一般形式是:
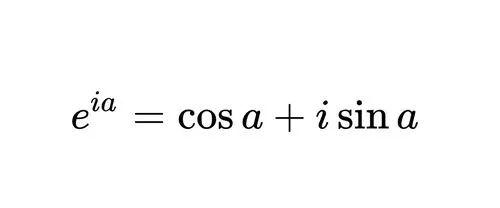
这里大家就可以发现数学上的三角公式与和表示e的X次方在某种程度上是等价的,只需要一个简单的基底变换就可以。
但是这两者的计算难度,明显不是一个数量级的。而且如果只是一个简谐波,那么用三角函数作为基底是没有问题的。但一旦涉及不同波的相互作用、波本身的衰减放大、非简谐情况,那么三角函数的表示计算就会过于复杂。在量子力学里,波函数几乎都不是简谐波,都存在一定程度上的调制和再构,三角函数已经蹩脚到几乎完全不能进行有效计算的程度,所以波函数就只能用复数来表示了。
3、复数可能揭示什么宇宙内涵
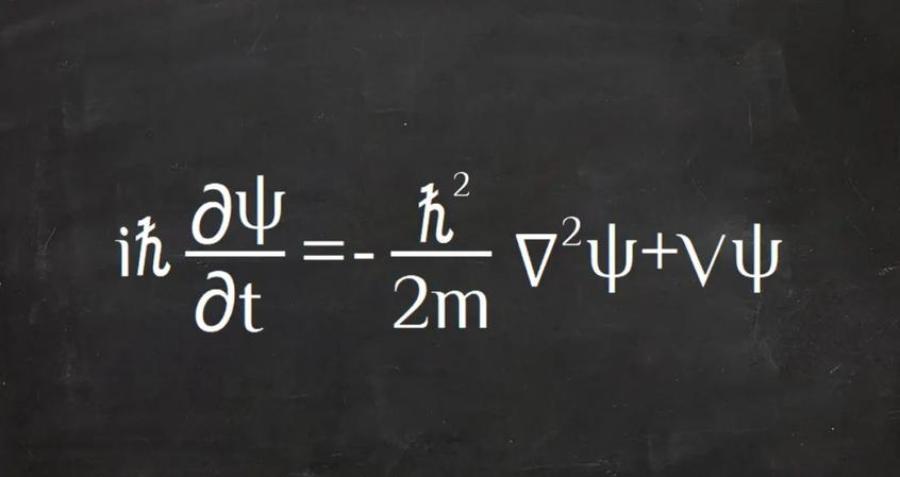
以上是薛定谔方程,可能非专业的人看到一定感觉是云里雾里,完全看不懂。想要读懂薛定谔方程,当然还需要更多数学物理背景知识。但是别的看不懂没关系,我们可以看到,这个方程里面就有一个i,这个线索告诉我们:
薛定谔方程是由复数体系来建立的。要知道,薛定谔方程可不是一个普通的方程,它可是号称宇宙方程的宇宙方程啊。
复数问题之所以重要,就是因为微观物理学的大厦是建立在量子力学的薛定谔方程的基础上的;薛定谔方程的是关于波函数的方程,而波函数是复数!
所以说,复数不仅应用广泛,能解决很多计算和描述上的问题,而且我们能强烈的感觉到,它的意义是非常深刻的,薛定谔方程的复数体系直指宇宙最深奥义。
4、复数是否对应某种物理实在?

近代物理不同于经典物理,量子力学的理论是基于复变量的希尔伯特空间实现的。如上,量子力学的波函数就是包含虚部的复数。所以,波函数确实有别于传统物理量的性质,它一般不通过试验观测得到,我们观测到的只是波函数的模的平方,只是个几率,这就与经典物理里的确定性完全不同。
复数在物理学中的作用是巨大的,甚至是根本的。可是,虚数对应什么样的物理存在呢?虚数描述什么物理现象呢?
这个问题的答案,很难回答,没有人明确的知道。
德国数学家莱布尼茨曾经感叹虚数的神奇,他说,“虚数是神灵遁迹的精微而奇异的隐避所,它大概是存在和虚妄两界中的两栖物”。
彭罗斯对复数物理意义也是充满疑惑,他在《通往实在之路》中写道:

“复数是本书中再三复现的主体,不止是因为这些数在数学上具有神奇性,更是因为自然本身在编织宇宙结构时利用了这种性质。但是我们还是要问一问:这难道真的就是我们这个世界的真实面貌?抑或只是这种数的数学性质导致了它们在物理理论中的大量应用?我相信许多物理学家倾向于第二种观点。但对他们来说仍有待解之谜,那就是为什么在量子力学框架内这些数会被运用的如此普遍,我们在基本的量子叠加原理中,在薛定谔方程、正频率条件、量子场论的无穷维‘复结构’中都遇到了复数。
不论怎样,我相信物理实在的数学基础问题无论从哪方面说都具有深刻的重要性”

彭罗斯在书中揭示了当前量子力学和宇宙学方面的大量理论难题。那么,波函数的本质到底是什么(与之相关,复数的物理意义何在)、意识在宇宙中究竟有什么地位。两者密切相关。
而复数的物理意义有可能是连接这两个问题的关键。

END