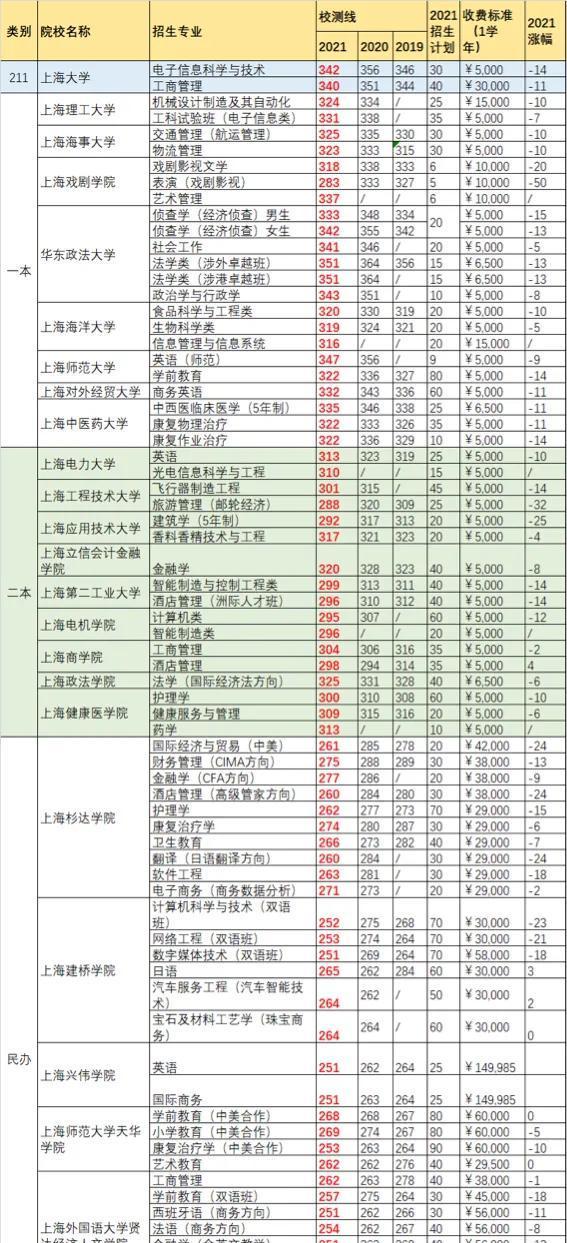
众所周知,做数据分析离不开统计学知识,它为我们的数据分析提供理论基础,然而很多数据分析师在学习统计学知识时感到头疼,看了很多统计学的书籍,里面讲了很多复杂的数学公式和推导,让人记不住也难理解,其实,市面上大部分的书籍都是面向高校教育的统计学书籍,专业性较强,对于数据分析师来说,我们并不需要掌握那么细。
因此,本文为大家列罗列了数据分析中需要掌握的统计学知识,让大家了解统计学有哪几大块,每一类分别用于什么样的分析场景,由于文章篇幅原因,仅为大家梳理知识点,具体的知识点讲解不详细展开。
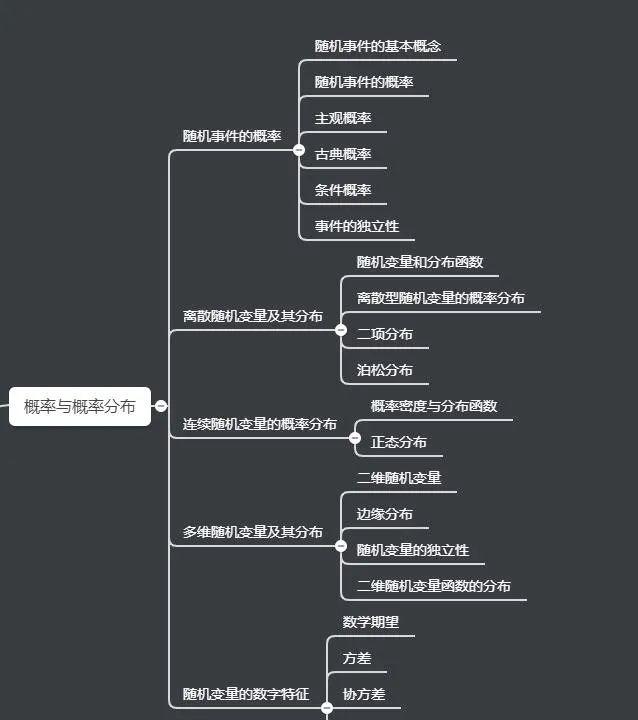
概率与概率分布
我的理解,《概率论与数理统计》更专业一些,偏理工科,会有大量公式的推导,知其然,知其所以然;而统计学这本书更基础,侧重于概念现象的解释,一般会直接给出结论,而不要求掌握结论的数理推导过程,文理科皆可用。
但不管是哪门课程,前期都是先讲概率和概率分布。概率论是统计学的基础,而随机事件的概率是概率论研究的基本内容。
统计学不研究统计,它研究的是不确定性。我们的世界是一个充满不确定性的环境,整个世界并非严格按照某个制定好的路线运行的。多数事物之间也并非有因必有果,万物之间充满了不可控的随机事件,我们不会因为今天努力了明天就一定会成功。
不确定性事件唯一的规律就是概率,独立随机事件我们没办法预测或控制它在某个时刻一定会发生,但却可以用概率来描述它发生的可能性。以概率论作为理论基础,为我们提供了认识不确定世界的方法。
这一章节,需要大家掌握几个核心概念:
随机事件
概率
概率分布
数字特征
用图表演示数据
工作中,一名数据分析师拿到了数据后,第一步要做的是数据初步探索,这也叫数据的预处理,这个时候,更多的就是利用各种图表探索数据。图表的好处是它可以很直观的看到数据的分布以及趋势,更有效的观察数据。
这一章节,需要大家掌握几个核心概念:
数据类型
统计表
统计图

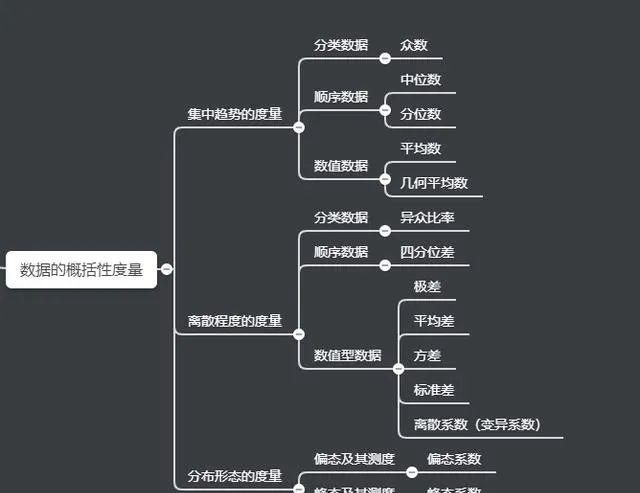
数据的概括性度量
利用上面所讲的图表展示,我们可以对数据分布的形状和特征有一个大致的了解,但要全面把握数据分布就要反映数据分布特征的代表值。通常包含分布的集中趋势、分布的离散程度、分布的形状。
数据分析中,最常见的场景,就是你手上拿到一组,一批或者一坨数据。不懂统计学的人,可能会不知所措,或者说,你不做些加工和处理,你不知道这些数据有啥用。这个时候,就需要通过这些概括性的度量指标,来帮我们从宏观上把握数据中的初步信息。
这一章节,需要大家掌握几个核心概念:
众数/平均数
方差/标准差
偏度/峰度
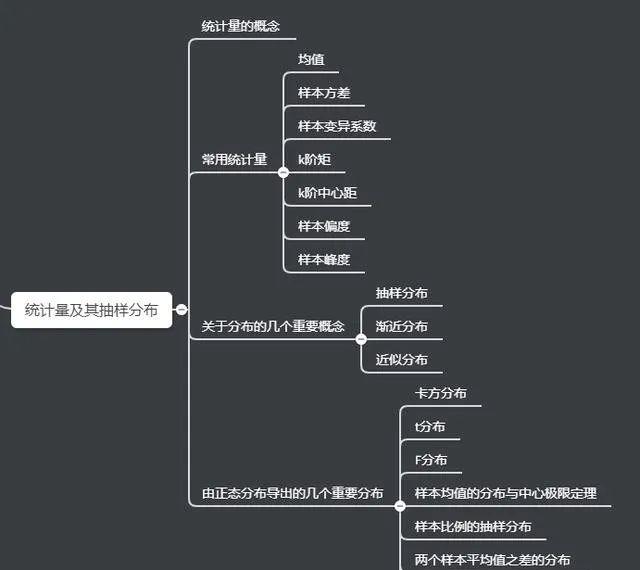
统计量及其抽样分布
抽样好懂,抽样分布不好懂。
抽样,就是从研究的总体中抽取一部分个体作为我们真正的研究对象,可以简单把样本理解为总体的一个子集,通过样本的结果来推测总体情况。比如我们想知道中国成年男性的平均身高,理论上最准确的办法是调查中国所有成年男性的身高,然后计算平均数。很显然,没人这样做。实际的做法总是抽取一部分人,然后计算这部分人的平均身高,由这个平均身高来大致估计总体的平均身高。
理解了抽样,再来理解抽样分布。抽样分布说的是对谁的分布?答案是样本统计量,比如样本均数或者样本比例。以样本均数为例,一般说样本均数的抽样分布如何如何,这里,样本均数被当成了一个随机变量来看待。我们最希望大家记住的要点:样本均数是一个随机变量,但对于初学者,这确实是比较反直觉的。
为何样本均数可以被当做一个随机变量?因为样本均数是依赖样本计算得出的:每抽取一组样本都可以计算出一个样本均数,而且这些样本均数或多或少都会有些差异。由此,样本均数会随着抽样的不同而随机变动。只是现实生活中我们一般只抽取一组样本,计算一个样本均数,因此,会觉得样本均数不变。
这一章节,需要大家掌握几个核心概念:
统计量
抽样
抽样分布
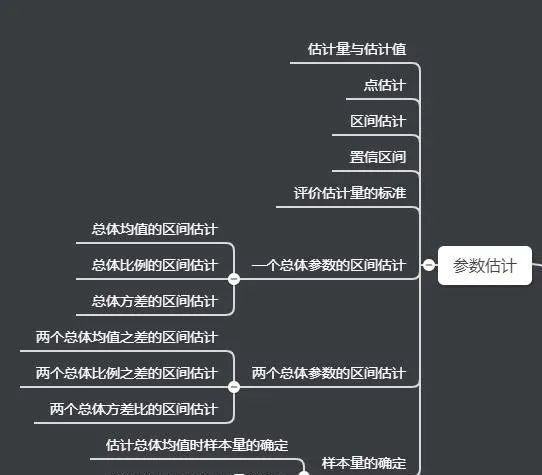
参数估计
当初大学里,学数理统计的时候,到了这块就感觉越来越难了,学习的过程中可以说就是囫囵吞枣,似懂非懂。但现在,经过漫长的实践过程,对统计学的知识有了更深一步的理解。
统计推断,说白了,就两件事。第一个,参数估计。第二个,各类假设检验。学习到这里,假如你是做数据挖掘,机器学习的,你就会强烈意识到,数据挖掘和统计学之间是存在千丝万缕的联系。
参数估计,顾名思义就是对参数进行估计,那什么是参数呢?就是你假设分布的参数就是说你认为或者知道某个随机过程服从什么分布,但是不确定他的参数是什么,那怎么办?你采样、采很多样本(实际值),通过这些样本的值去估计分布的参数就是参数估计。
这一章节,需要大家掌握几个核心概念:
参数
点估计
区间估计
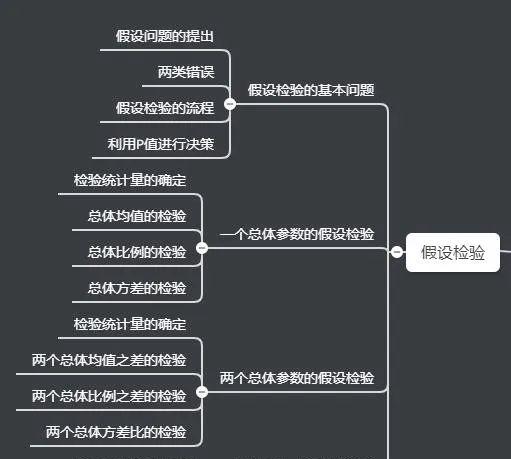
假设检验
上面讲到,统计推断就需要明白两件事,一件是参数估计,另外一件是假设检验。
假设检验是什么?说白了,假设检验就是先对总体猜一个参数值,然后利用样本的数据检验这个参数值准不准。
互联网生产实践中的ABTEST方法,就经常会应用到假设检验的思想。
举一个简单的例子:
学而思网校App进行了改版迭代,现在有以下两个版本
版本1:首页为一屏课程列表
版本2:首页为信息流
如果我们想区分两个版本,哪个版本用户更喜欢,转化率会更高。我们就需要对总体(全部用户)进行评估,但是并不是全部存量用户都会访问App,并且每天还会新增很多用户,所以我们无法对总体(全部用户)进行评估,我们只能从总体的用户中随机抽取样本(访问App)的用户进行分析,用样本数据表现情况来充当总体数据表现情况,以此来评估哪个版本转化率更高。
这一章节,需要大家掌握几个核心概念:
假设检验
P值
回归分析
大学里学习统计学的时候,最喜欢学回归分析,也是学的最明白的一部分。因为它的易懂性,也因为它的实用性。但随着自己数据分析经验的积累,对回归分析的理解也越来越深,它不是简单的回归模型求解那么简单,它更是一种日常工作中解决问题的思路和方法论。
数据挖掘中使用的各种高深的模型,任何模型都可理解成回归模型,包含因变量Y和自变量X,求解参数。
在我看来,回归分析由两部分组成:业务分析和技术分析。其中,业务分析属于“道”的层面,而技术分析属于“术”的层面。从“道”的层面来看,回归分析是业务分析,其分析的不是数据,而是业务,是业务中的不确定性。通过业务分析,获得对业务不确定性的理解,进而将抽象的不确定性业务问题转换成一个具体的数据可分析问题。
什么是数据可分析问题?一个业务问题,只要有清晰定义的因变量Y(不管是看得见的,还是看不见的)和清晰定义的自变量X,这就是一个数据可分析问题。一旦把业务问题规范成一个具体的数据可分析问题(有清晰定义的Y和X),那么接下来就是技术分析,属于回归分析“术”的层面。在这个层面,人们关心对于一个既定的Y和X,要研究其中的不确定性,应该选择什么样的模型设定,线性模型还是非线性模型,一元模型还是多元模型,简单的决策树还是随机森林,普通的神经网络还是深度学习。模型设定确定下来后,还需思考应该用什么方法估计,如何调优,等等。
以上是对回归分析的一种广义上的理解,狭义上理解回归分析,需要理解以下几个核心概念:
相关系数
回归分析
最小二乘法
显著性检验
多重共线性
拟合优度

当然,统计学的知识还包含很多,比如方差分析,时间序列分析,统计指数等等,这些知识在特定的应用场合,也有着广泛的应用,只是相比以上的知识点,应用范围更小点。