图的深度优先遍历算法(图的深度优先遍历定义)-众学网

1. 什么是图论

图论（英语：Graph theory），是组合数学的一个分支，和其他数学分支，如群论、矩阵论、拓扑学有着密切关系。图是图论的主要研究对象。图是由若干给定的顶点及连接两顶点的边所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物，连接两顶点的边则用于表示两个事物间具有这种关系。

图论起源于著名的柯尼斯堡七桥问题。该问题于1736年被欧拉解决，因此普遍认为欧拉是图论的创始人。

图论的研究对象相当于一维的单纯复形。

—维基百科的定义

2. 图的两种形式遍历

所谓图的遍历（graph traversal），也称为搜索（search），就是从图中某个顶点出发，沿着一些边访遍图中所有的顶点，且使每个顶点仅被访问一次。遍历可以采取两种方法进行：深度优先搜索（DFS，depth first search）

和广度优先搜索（BFS，breadth first search）。

3. 图的深度优先遍历顺序

深度优先搜索是一个递归过程，有回退过程。DFS 算法的思想是：对一个无向连通图，在访问图中某一起始顶点 v 后，由 v 出发，访问它的某一邻接顶点w1；再从w1出发，访问与w1邻接但还没有访问过的顶点w2；然后再从w2出发，进行类似的访问；…；如此进行下去，直至到达所有邻接顶点都被访问过的顶点u为止；接着，回退一步，回退到前一次刚访问过的顶点，看

是否还有其它没有被访问过的邻接顶点，如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问；如果没有，就再回退一步进行类似的访问。重复上述过程，直到该连通图中所有顶点都被访问过为止。

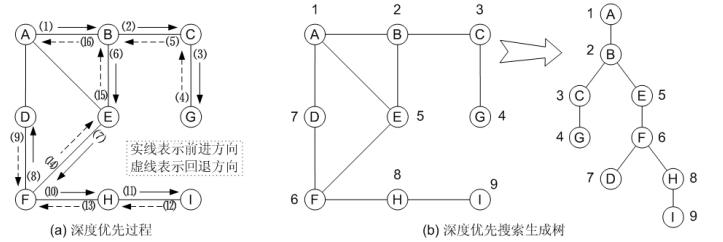
深度优先遍历的递归的遍历形式:

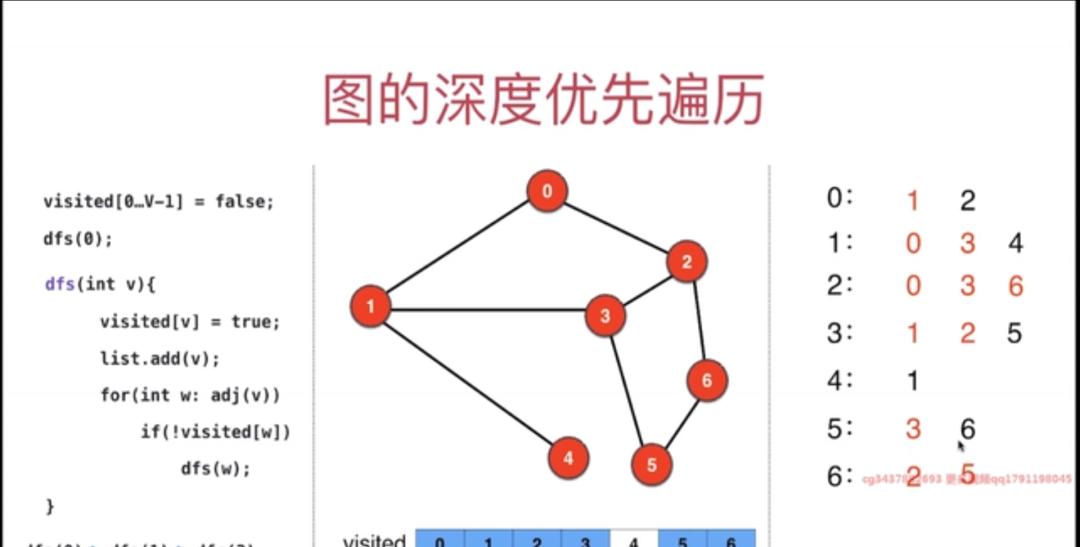
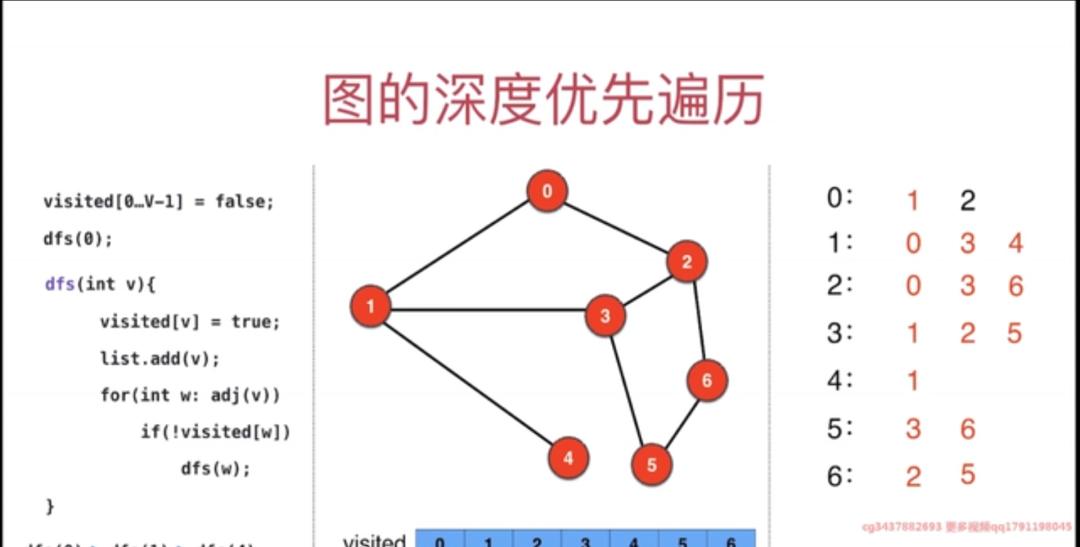
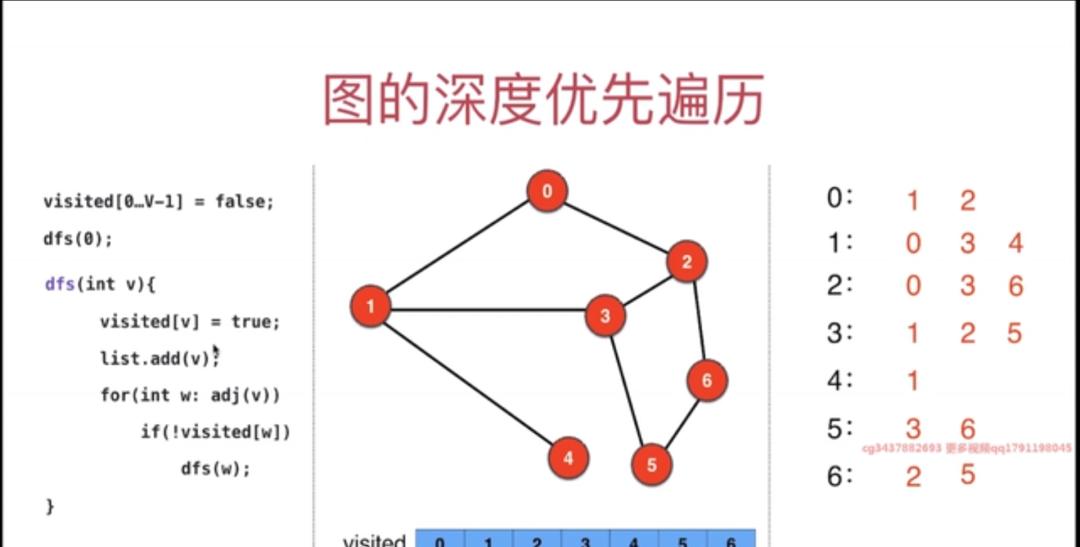
4. 图的深度优先遍历伪代码

树的前序遍历，与图的深度优先遍历的比较：

5. 实现图的深度优先遍历

连通图的深度优先遍历

-结合上述的伪代码

package graphDFS;import java.util.ArrayList;public class GraphDFS { // 创建一个数组， private ArrayList<Integer> res = new ArrayList<>(); // 输出最后深度优先遍历的结果 private boolean[] visited; private Graph graph; public GraphDFS(Graph graph) { this.graph = graph; visited = new boolean[graph.V()]; // 结点的数量 dfs(0); } private void dfs(int v) { visited[v] = true; res.add(v); for (int w: graph.adj(v)) { // 遍历该节点的相邻结点 if (! visited[w]) dfs(w); } } public Iterable<Integer> res(){ return res; } public static void main(String[] args) { Graph graph = new Graph(“g2.txt”); GraphDFS graphDFS = new GraphDFS(graph); System.out.println(graphDFS.res());// [0, 1, 3, 2, 6, 5, 4] }}

6. 遍历图的深度优先遍历的改进

如果不是联通图的话，孤立的结点将不会遍历。

-结合上述的伪代码

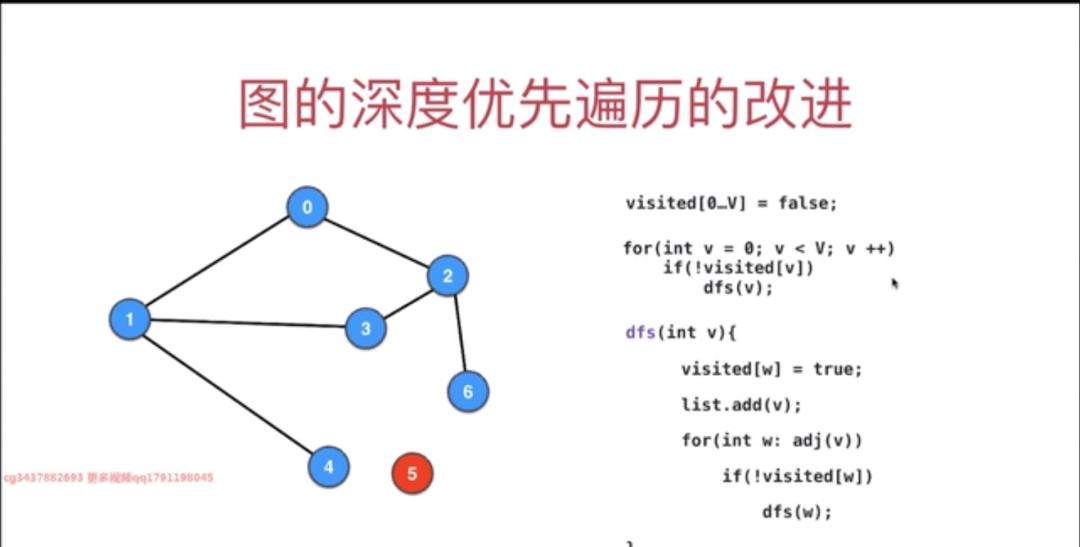
package graphDFS;import java.util.ArrayList;public class GraphDFS { // 创建一个数组， private ArrayList<Integer> res = new ArrayList<>(); // 输出最后深度优先遍历的结果 private boolean[] visited; private Graph graph; public GraphDFS(Graph graph) { this.graph = graph; visited = new boolean[graph.V()]; // 结点的数量 //dfs(0); // 改进的地方：对每一个结点进行遍历 for (int v = 0; v < graph.V(); v ) { if (!visited[v]) { dfs(v); } } } private void dfs(int v) { visited[v] = true; res.add(v); for (int w: graph.adj(v)) { // 遍历该节点的相邻结点 if (! visited[w]) dfs(w); } } public Iterable<Integer> res(){ return res; } public static void main(String[] args) { Graph graph = new Graph(“g2.txt”); GraphDFS graphDFS = new GraphDFS(graph); System.out.println(graphDFS.res());// [0, 1, 3, 2, 6, 5, 4] }}

1.一起玩转图论算法之一：图的基本表示

END