看一道希望杯培训试题:

题目:一个自然数,在3进制中的数字和是24。它在9进制中的数字和最小是____,最大是____.
很明显,这是一个进制问题,在讲本讲之前,回顾一下黄老师以前讲过的进制转换!:十进制与二进制的互相转换
上一讲讲了二进制、十进制的相互转换,其中半斤等于八两就是十进制与十六进制的转换!
上一讲留下的练习就是本讲的题目,好,那么此题如何解?
解:我们先列出一些数,看一下这些数的3进制和9进制有什么区别:
比如说先把1到9这九个数字用三进制和九进制来表达一下:
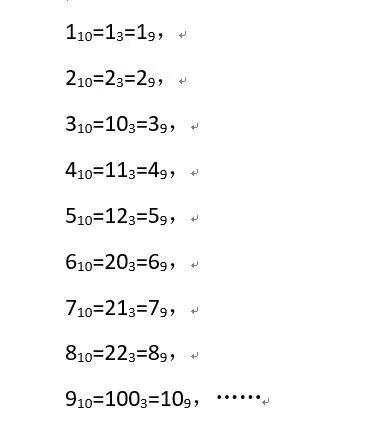
我们可以发现,3进制与9进制有一定的对应关系,即从末位向前每2位3进制可对应1位9进制 ;相应的数字和至少是相等的,而最大可以是3倍的关系,例如:

按此规律,9进制中数字和最小为24,最大为24×3=72。
好吧,不得不说,此种方法需要较强的推理能力和运气,最大三倍也只是在小部分数字中归纳总结出来的规律,没有严格的证明,所以,如果是解答题,此解法还不是很完善。
我们是否可以通过列举法来解这个题呢?
那么,我们需要把3进制中所有数字和为24的都写出来,而这是写不完的。。。
比如222222222222,这是一个三进制数,所有数字和也为24,但,任意两个“2”中间加上一个或多个“0”,同样也是三进制数,所有数字和也是24,但这样的数是无穷无尽的,所以本题列举法不可能实现,列举法也是为了归纳总结做准备。