本文具体的实例来讲一下如何进行线性和非线性拟合，希望对大家有所帮助。
01
非线性拟合
本部分简单示范下Origin非线性拟合的方法，挺好用，比excel 强多了。使用的origin是8.0版，不同的版本操作可能有点不同，但结果差不多。
1
例一
打开界面，输入数据，拟合表面张力对浓度曲线那一题。如下图：
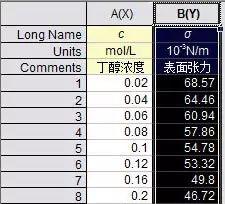
图1 选择数据
作出散点图:Plot/Symbol/Scatter，发现不是线性的……
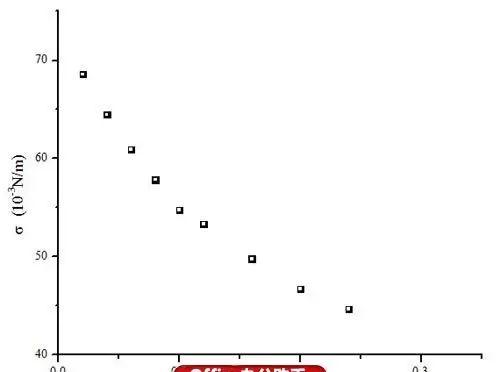
图2 散点图
这时要稍微考虑一下，拟合的方法可以选择多项式拟合，在Excel里也可以做的，而且项数越多，相关系数越大。根据级数的概念，项数无限多时候，R2是可以为1的。查阅一下物化下册的教材，发现这个公式：
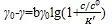，(西施科夫斯基公式)，经过稍微变形，转化为
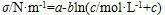，a、b、c是参数，都有明确的意义，另一个c是浓度。这时用对数函数就可以方便地拟合了，在工具栏依次选Analysis/Fitting/Nonlinear Curve Fit/Open Dialogue…，在弹出的窗口中，Function Selection部分的Category选择Logarithm，Function选择Log3P1，因为这个函数形式正好是y=a-bln(x c),从下面的Formula可以看到：
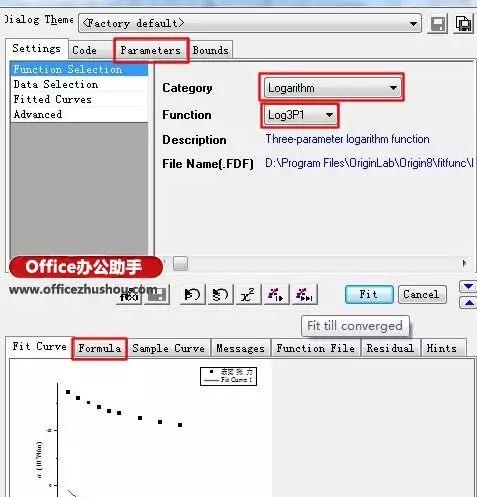
图3 选择函数
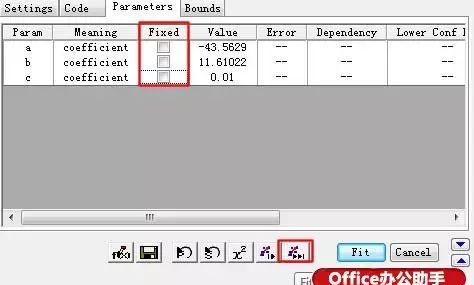
图4
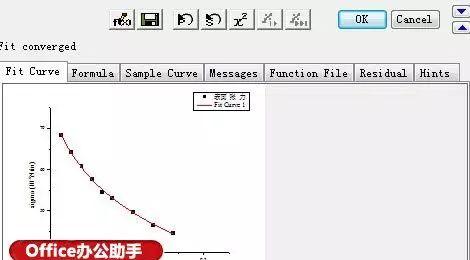
图5
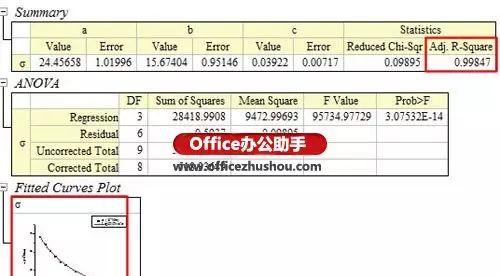
图6 弹出的参数
双击上图中左下角的图形，弹出最终拟合的曲线：
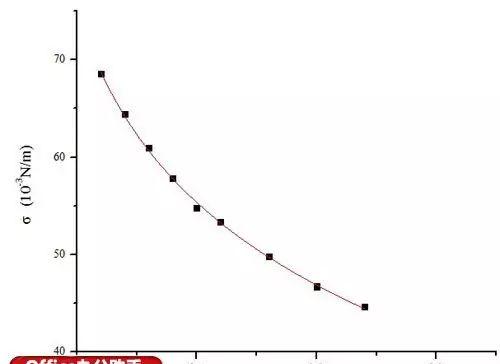
图7 最终拟合曲线
至此，拟合完毕。
2
例二
下一题乙醇黏度的二元拟合，先把那90个数据全部输入，下图只截了前15个数据：
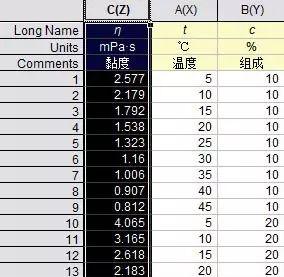
图8 输入数据
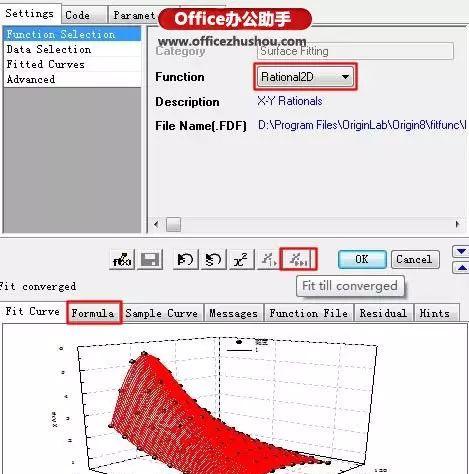
图9 选择Rational2D函数
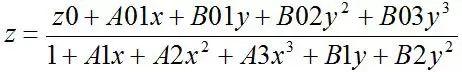
图10 Rational2D的公式(x对应温度，y对应组成，z对应黏度)
ok后，也会弹出参数，对照上面的公式，抄一下参数，公式太复杂，不知道各项是什么意思，或者根本没有意义的。双击图形，稍微调整下就行了：
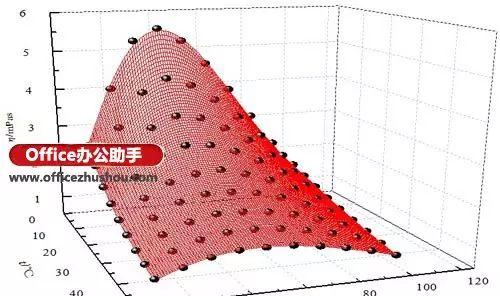
图11 最终拟合图形
这两个图弄出来后，就可以高兴地去打印了。
02
线性拟合
线性拟合作为数学计算中一种常用的数学方法，在建筑、物理、化学、甚至于天体物理、航天中都得到基本的应用。线性拟合是指用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之间的函数关系。
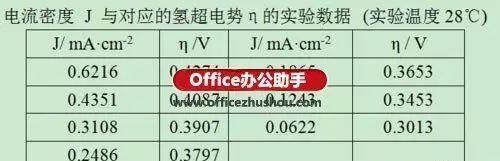
本文以氢超电势的测定实验数据处理为例，按照数据处理及线性拟合两部分介绍将相关实验数据使用Origin软件进行线性拟合的方法。
1
数据处理
1、把数据导入Origin或输入到Origin：
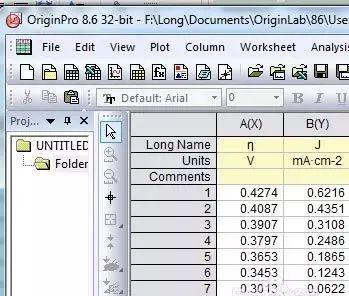
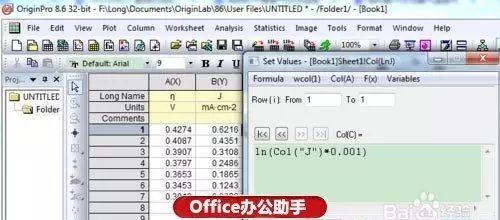
3、选中第一列和第三列作散点图，即A、C两列：
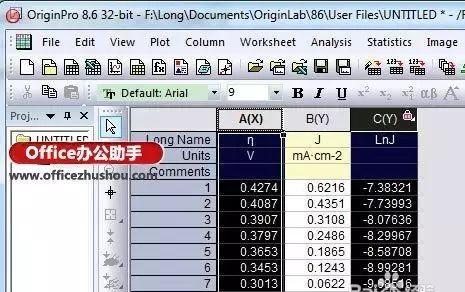
4、做出的散点图如下：
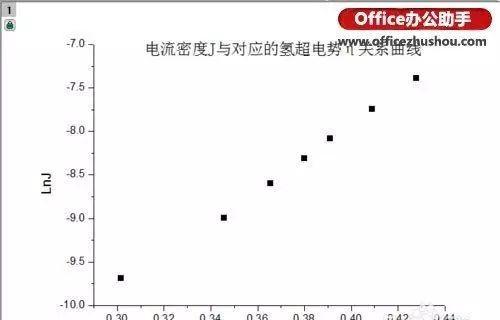
2
线性拟合
1、选择数据点——“Analysis”——“Fitting”——“Linear Fit”：
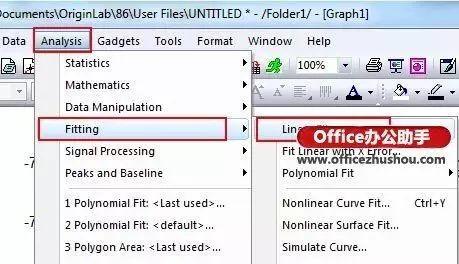
2、弹出线性拟合对话框：
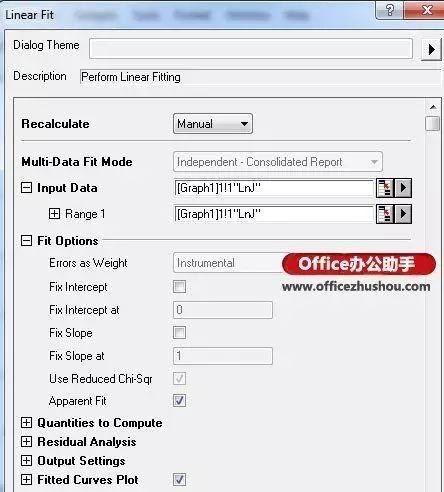
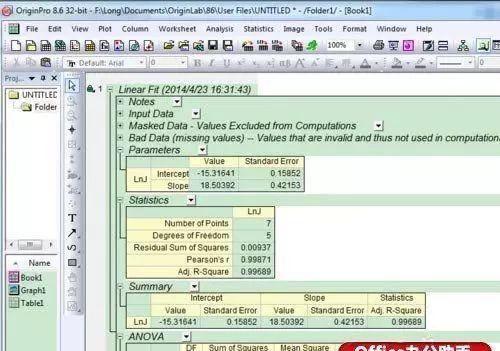
4、自动跳转到线性拟合结果分析表：
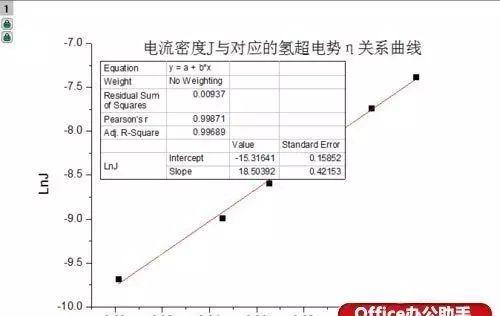
本文来自“Office办公助手”。
