对角矩阵和三角矩阵
一、 对角矩阵
只有对角线上有非0元素的矩阵称为对角矩阵,对角线上的元素相等的对角矩阵称为数量矩阵,对角线上的元素都为1的对角矩阵称为单位矩阵。
(1)提取矩阵的对角线元素,diag(A)函数用于提取矩阵A的对角线元素,产生一个具有min(m,n)个元素的向量,diag(A,k)提取第k条对角线上的元素,对角线上向上为第1条,向下为第-1条。

(2)构造对角矩阵,设A为具有m个元素的向量,diag(A)将产生一个m行m列的对角矩阵,则对角线上的元素即为A的元素,diag(A,k),产生一个n行n列的对角矩阵(n=m |k|)。

二、三角矩阵
三角矩阵分为上三角矩阵和下三角矩阵,上三角矩阵是对角线以下元素全为0的矩阵,下三角矩阵是对角线以上元素全为0的矩阵
(1)提取矩阵A的上三角矩阵,triu(A)产生矩阵B,矩阵B与A同型,矩阵B对角线以上的元素与A一一对应,对角线以下的元素全为0,triu(A,k),求矩阵第k条对角线以上的元素。

(2)提取矩阵A的下三角矩阵,tril(A)产生矩阵B,矩阵B与A同型,矩阵B对角线以下的元素与A一一对应,对角线以上的元素全为0,tril(A,k),求矩阵第k条对角线以下的元素。

二
矩阵的转置与旋转
一· 矩阵的转置
把原矩阵的第1行变成新矩阵的第1列,第2行变成第2列,以此类推,一个m行n列矩阵经过转置变换成一个n行m列的矩阵,转置运算符是单撇号(’)。
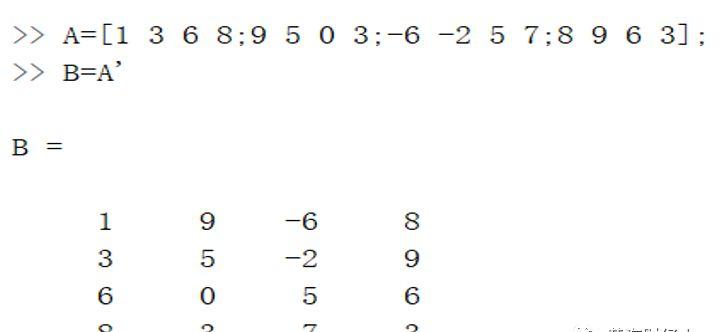
二·矩阵的旋转
以90°为单位把原矩阵按逆时针方向旋转,rot90(A,k)将矩阵A按逆时针旋转90°的k次。

三·矩阵的左右翻转
将原矩阵的第一列和最后一列调换,第二列和倒数第二列调换,以此类推,利用fliplr(A)实现。

四· 矩阵的上下翻转
将原矩阵的第一行和最后一行调换,第二行和倒数第二行调换,以此类推,利用flipud(A)实现。

三
矩阵的逆
一·矩阵的逆
对于一个方阵A,如果存在一个与其同阶的方阵B,使得A*B=B*A=E(单位矩阵),则称B为A的逆矩阵,A为B的逆矩阵,可调用函数int(A)。
例:用求逆矩阵的方法求解线性方程组
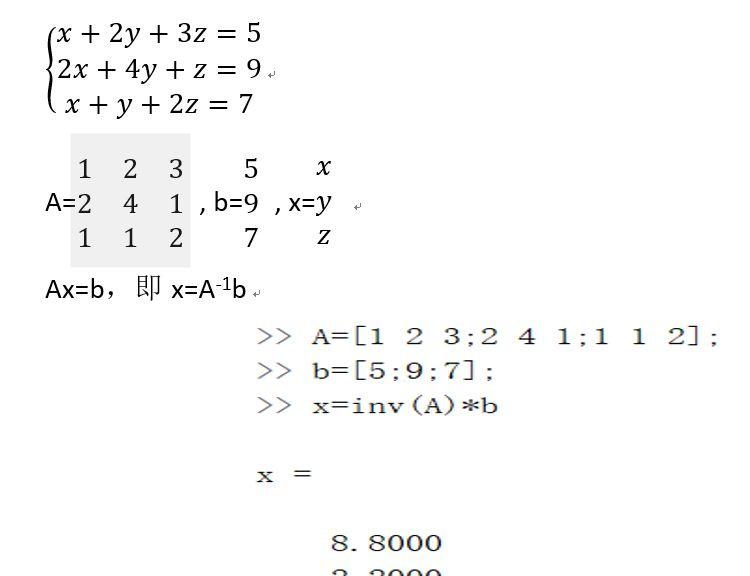
四
矩阵的求值
一· 方阵的行列式
把一个方阵看成一个行列式,并对其按行列式的规则求值,这个值就是矩阵所对应的行列式的,用函数det(A)进行实现。

二·矩阵的秩和迹
(1)矩阵的秩
对于m*n阶的矩阵A,如果m个行向量中有r(r<=m)个行向量线性无关,而其余为线性相关,则称r为矩阵A的行秩,用函数rank(A)可以求得矩阵的秩。

(2)矩阵的迹
矩阵的迹等于矩阵的对角线元素之和也等于矩阵的特征值之和,用trace(A)求矩阵的迹。

五
课后练习
求下列矩阵的主对角线元素、上三角矩阵、下三角矩阵、逆矩阵、行列式的值、秩、迹、矩阵的转置。
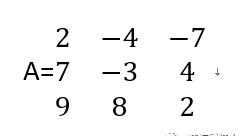
撰稿|财经学院
审核|李娇娇 责编|孙雨