
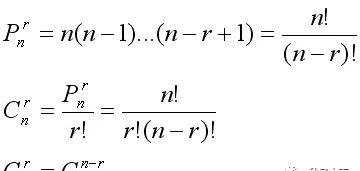
公式P是指排列,从N个元素取R个进行排列。公式C是指组合,从N个元素取R个,不进行排列。N-元素的总个数R参与选择的元素个数!-阶乘 ,如 9!=9*8*7*6*5*4*3*2*1
从N倒数r个,表达式应该为n*(n-1)*(n-2)..(n-r 1);
因为从n到(n-r 1)个数为n-(n-r 1)=r
举例:
Q1:有从1到9共计9个号码球,请问,可以组成多少个三位数?
A1: 123和213是两个不同的排列数。即对排列顺序有要求的,既属于“排列P”计算范畴。
上问题中,任何一个号码只能用一次,显然不会出现988,997之类的组合, 我们可以这么看,百位数有9种可能,十位数则应该有9-1种可能,个位数则应该只有9-1-1种可能,最终共有9*8*7个三位数。计算公式=P(3,9)=9*8*7,(从9倒数3个的乘积)
Q2:有从1到9共计9个号码球,请问,如果三个一组,代表“三国联盟”,可以组合成多少个“三国联盟”?
A2: 213组合和312组合,代表同一个组合,只要有三个号码球在一起即可。即不要求顺序的,属于“组合C”计算范畴。
上问题中,将所有的包括排列数的个数去除掉属于重复的个数即为最终组合数C(3,9)=9*8*7/3*2*1
排列、组合的概念和公式典型例题分析
例1 设有3名学生和4个课外小组.(1)每名学生都只参加一个课外小组;(2)每名学生都只参加一个课外小组,而且每个小组至多有一名学生参加.各有多少种不同方法?
解(1)由于每名学生都可以参加4个课外小组中的任何一个,而不限制每个课外小组的人数,因此共有种不同方法.
(2)由于每名学生都只参加一个课外小组,而且每个小组至多有一名学生参加,因此共有种不同方法.
点评 由于要让3名学生逐个选择课外小组,故两问都用乘法原理进行计算.
例2排成一行,其中不排第一,不排第二,不排第三,不排第四的不同排法共有多少种?
解 依题意,符合要求的排法可分为第一个排、、中的某一个,共3类,每一类中不同排法可采用画“树图”的方式逐一排出:
∴ 符合题意的不同排法共有9种.
点评 按照分“类”的思路,本题应用了加法原理.为把握不同排法的规律,“树图”是一种具有直观形象的有效做法,也是解决计数问题的一种数学模型.
例3 判断下列问题是排列问题还是组合问题?并计算出结果.
(1)高三年级学生会有11人:①每两人互通一封信,共通了多少封信?②每两人互握了一次手,共握了多少次手?
(2)高二年级数学课外小组共10人:①从中选一名正组长和一名副组长,共有多少种不同的选法?②从中选2名参加省数学竞赛,有多少种不同的选法?
(3)有2,3,5,7,11,13,17,19八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?
(4)有8盆花:①从中选出2盆分别给甲乙两人每人一盆,有多少种不同的选法?②从中选出2盆放在教室有多少种不同的选法?
分析 (1)①由于每人互通一封信,甲给乙的信与乙给甲的信是不同的两封信,所以与顺序有关是排列;②由于每两人互握一次手,甲与乙握手,乙与甲握手是同一次握手,与顺序无关,所以是组合问题.其他类似分析.
(1)①是排列问题,共用了封信;②是组合问题,共需握手(次).
(2)①是排列问题,共有(种)不同的选法;②是组合问题,共有种不同的选法.
(3)①是排列问题,共有种不同的商;②是组合问题,共有种不同的积.
(4)①是排列问题,共有种不同的选法;②是组合问题,共有种不同的选法.
例4 证明.
证明 左式
右式.
∴ 等式成立.
点评 这是一个排列数等式的证明问题,选用阶乘之商的形式,并利用阶乘的性质,可使变形过程得以简化.
例5 化简.
解法一 原式
解法二 原式
点评 解法一选用了组合数公式的阶乘形式,并利用阶乘的性质;解法二选用了组合数的两个性质,都使变形过程得以简化.
例6 解方程:(1);(2).
解 (1)原方程
解得.
(2)原方程可变为
∵ ,,
∴ 原方程可化为.
即 ,解得
第六章排列组合、二项式定理
一、考纲要求
1.掌握加法原理及乘法原理,并能用这两个原理分析解决一些简单的问题.
2.理解排列、组合的意义,掌握排列数、组合数的计算公式和组合数的性质,并能用它们解决一些简单的问题.
3.掌握二项式定理和二项式系数的性质,并能用它们计算和论证一些简单问题.
二、知识结构
三、知识点、能力点提示
(一)加法原理乘法原理
说明加法原理、乘法原理是学习排列组合的基础,掌握此两原理为处理排 列、组合中有关问题提供了理论根据.
例15位高中毕业生,准备报考3所高等院校,每人报且只报一所,不同的报名方法共有多少种?
解: 5个学生中每人都可以在3所高等院校中任选一所报名,因而每个学生都有3种不同的 报名方法,根据乘法原理,得到不同报名方法总共有
3×3×3×3×3=35(种)
(二)排列、排列数公式
说明排列、排列数公式及解排列的应用题,在中学代数中较为独特,它研 究的对象以及研 究问题的方法都和前面掌握的知识不同,内容抽象,解题方法比较灵活,历届高考主要考查排列的应用题,都是选择题或填空题考查.
例2由数字1、2、3、4、5组成没有重复数字的五位数,其中小于50000的 偶数共有()
A.60个B.48个C.36个D.24个
解因为要求是偶数,个位数只能是2或4的排法有P12;小于50 000的五位数,万位只能是1、3或2、4中剩下的一个的排法有P13;在首末两位数排定后,中间3个位数的排法有P33,得P13P33P12=36(个)
由此可知此题应选C.
例3将数字1、2、3、4填入标号为1、2、3、4的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不同的填法有多少种?
解:将数字1填入第2方格,则每个方格的标号与所填的数字均不相同的填法有3种,即214 3,3142,4123;同样将数字1填入第3方格,也对应着3种填法;将数字1填入第4方格,也对应3种填法,因此共有填法为
3P13=9(种).
例四 例五可能有问题,等思考
三)组合、组合数公式、组合数的两个性质
说明历届高考均有这方面的题目出现,主要考查排列组合的应用题,且基本上都是由选择题或填空题考查.
例4从4台甲型和5台乙型电视机中任意取出3台,其中至少有甲型与乙型电视机各1台,则不同的取法共有()
A.140种B.84种C.70种D.35种
解:抽出的3台电视机中甲型1台乙型2台的取法有C14·C25种;甲型2台乙型1台的取法有C24·C15种
根据加法原理可得总的取法有
C24·C25 C24·C15=40 30=70(种 )
可知此题应选C.
例5甲、乙、丙、丁四个公司承包8项工程,甲公司承包3项,乙公司承包1 项,丙、丁公司各承包2项,问共有多少种承包方式?
解:甲公司从8项工程中选出3项工程的方式 C38种;
乙公司从甲公司挑选后余下的5项工程中选出1项工程的方式有C15种;
丙公司从甲乙两公司挑选后余下的4项工程中选出2项工程的方式有C24种;
丁公司从甲、乙、丙三个公司挑选后余下的2项工程中选出2项工程的方式有C22种.
根据乘法原理可得承包方式的种数有C38×C15×C24×C22=×1=1680(种).
(四)二项式定理、二项展开式的性质
说明二项式定理揭示了二项式的正整数次幂的展开法则,在数学中它是常用的基础知识,从1985年至1998年历届高考均有这方面的题目出现,主要考查二项展开式中通项公式等,题型主要为选择题或填空题.
例6在(x-)10的展开式中,x6的系数是()
A.-27C610B.27C410C.-9C610D.9C410
解设(x-)10的展开式中第γ 1项含x6,
因Tγ 1=Cγ10×10-γ(-)γ,10-γ=6,γ=4
于是展开式中第5项含x 6,第5项系数是C410(-)4=9C410
故此题应选D.
例7(x-1)-(x-1)2+(x-1)3-(x-1) (x-1)5的展开式中的x2的系数等于
解:此题可视为首项为x-1,公比为-(x-1)的等比数列的前5项的和,则其和为
在(x-1)6中含x3的项是C36x3(-1)3=-20×3,因此展开式中x2的系数是-2 0.
(五)综合例题赏析
例8若(2x )4=a0 a1x a2x2 a3x3 a4x4,则(a0 a2 a4)2-(a1 a3)2的值为()
A.1B.-1C.0D.2
解:A.
例92名医生和4名护士被分配到2所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有()
A.6种B.12种C.18种D.24种
解分医生的方法有P22=2种,分护士方法有C24=6种,所以共有6×2=12种不同的分配方法。
应选B.
例10从4台甲型和5台乙型电视机中任意取出3台,其 中至少要有甲型与乙型电视机各1台,则不同取法共有().
A.140种B.84种C.70种D.35种
解:取出的3台电视机中,甲型电视机分为恰有一台和恰有二台两种情形.
∵C24· C25·C14=5×6 10×4=70.
∴应选C.
例11某小组共有10名学生,其中女生3名,现选举2 名代表,至少有1名女生当选的不同选法有()
A.27种B.48种C.21种D.24种
解:分恰有1名女生和恰有2名女生代表两类:
∵C13·C17 C23=3×7 3=24,
∴应选D.
例12由数学0,1,2,3,4,5组成没有重复数字的 六位数,其中个位数字小于十位数字的共有().
A.210个B.300个
C.464个D.600个
解:先考虑可组成无限制条件的六位数有多少个?应有P15·P 55=600个.
由对称性,个位数小于十位数的六位数和个位数大于十位数的六位数各占一半.
∴有×600=300个符合题设的六位数.
应选B.
例13以一个正方体的顶点为顶点的 四面体共有().
A.70个B.64个
C.58个D.52个
解:如图,正方体有8个顶点,任取4个的组合数为C48=70个.
其中共面四点分3类:构成侧面的有6组;构成垂直底面的对角面的有2组;形如(ADB1C1)的有4组.
∴能形成四面体的有70-6-2-4=58(组)
应选C.
例14如果把两条异面直线看成“一对”,那么六棱 锥的棱所在的12条直线中,异面直线共有().
A.12对B.24对
C.36对D.48对
解:设正六棱锥为O—ABCDEF.
任取一侧棱OA(C16)则OA与BC、CD、DE、EF均形成异面直线对.
∴共有C16×4=24对异面直线.
应选B.
例15正六边形的中心和顶点共7个点,以其中三个点 为顶点的三角形共个(以数字作答).
解:7点中任取3个则有C37=35组.
其中三点共线的有3组(正六边形有3条直径).
∴三角形个数为35-3=32个.
例16设含有10个元素的集合的全部子集数为S,其中由3个元素组成的子集数为T,则的值为。
解 10个元素的集合的全部子集数有:
S=C010 C110 C210 C310 C410 C510 C610 C710 C810 C910 C1010=210=1024
其中,含3个元素的子集数有T=C310=120
故=
例17例17在50件产品 n 中有4件是次品,从中任意抽了5件 ,至少有3件是次品的抽法共
种(用数字作答).
解:“至少3件次品”即“有3件次品”或“有4件次品”.
∴C34·C246 C44·C146=4186(种)
例18有甲、乙、丙三项任务,甲需2人承担,乙、 丙各需1人承担,从10人中选派4人承担这三项任务,不同的选法共有().
A.1260种B.2025种
C.2520种D.5040种
解:先从10人中选2个承担任务甲(C210)
再从剩余8人中选1人承担任务乙(C18)
又从剩余7人中选1人承担任务乙(C17)
∴有C210·C18C17=2520(种).
应选C.
例19集合{1,2,3}子集总共有().
A.7个B.8个C.6个D.5个
解三个元素的集合的子集中,不含任何元素的子集有一个,由一个元素组成的子集数
C13,由二个元素组成的子集数C23。
由3个元素组成的子集数C33。由加法原理可得集合子集的总个数是
C13 C23 C33 1=3 3 1 1=8
故此题应选B.
例20假设在200件产品中有3件是次品,现在从中任意抽取5件,其中至少有两件次品的抽法有().
A.C23C3197种B.C23C3197 C33C2197
C.C5200-C5197D.C5200-C13C4197
解:5件中恰有二件为次品的抽法为C23C3197,
5件中恰三件为次品的抽法为C33C2197,
∴至少有两件次品的抽法为C23C3197 C33C2197.
应选B.
例21两排座位,第一排有3个座位,第二排有5个座位,若8名学生入座(每人一个座位),则不同座法的总数是().
A.C58C38B.P12C58C38C.P58P38
猜您喜欢往期精选▼
1.女生头像霸气 个性霸气女生头像
2.女生动漫头像 御姐动漫女生头像
4.手机投屏电视怎么设置 一招教你手机如何投屏到电视上
5.肖战视频专访 正面回应227事件,先后两次进行道歉
6.2020情侣头像情侣专用 情侣头像真人一人一半
7.闺蜜头像两人一人一张|两人四人闺蜜头像
8.谷歌卫星地图2020年高清最新版>>>
9.安全教育平台登录入口 安全教育平台我的作业
10.脑筋急转弯大全及答案爆笑版 脑筋急转弯大全及答案(搞笑版)










