下图所示为一个圆柱被一个倾斜的平面α所截,天蓝色曲线为截痕,这里用p表示。我们先要简单证明这个截痕为椭圆。然后把圆柱面沿一条母线剪开并展平,则椭圆变成了一条正弦曲线的一个周期。最后还要简单说一下椭圆积分。您是不是觉得椭圆积分有些太过高深?是的。但椭圆积分名称的得来,则与本篇求椭圆的周长有关。
1. 在圆柱内部切割面的上下,各放一个球C1和C2(图中都只画了一半,够用了),球与切割面和圆柱侧面均相切。两球与切割面相切之点分别为F1和F2。在截痕p上取一点P。根据球外一点到球的所有切线的长度相等,可以得出
PF1=PQ1;PF2=PQ2
而
PQ1 PQ2=Q1Q2 (粉色线段)=O1O2
是定长,所以,截痕p(当然是平面图形)上任意一点P到点F1和F2(都是定点)的距离之和为定长。所以,截痕p是椭圆。这个椭圆的四个顶点分别是A1、A2、B1和B2。显然,线段B1B2即短轴长2b等于圆柱底面直径2r。所以b=r。见下图。
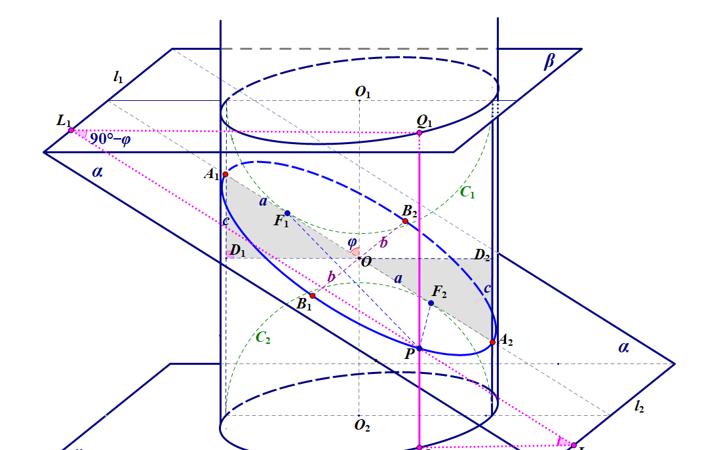
设圆O1和O2(球与圆柱面相切之圆)所在平面β和γ与切割面分别交于直线l1和l2。过点P作l1的垂线,垂足为L1。则三角形PL1Q1(粉色)为直角三角形,且角L1PQ1等于切割面与圆柱中轴线的夹角φ。点P可动,但这样的直角三角形都是相似的。这说明,
PF1:PL1=PQ1:PL1=cosφ=常数
这正符合圆锥曲线的统一定义,其中椭圆的定义为:当一个动点到一个定点的距离与到一条定直线的距离的比值是一个大于0小于1的数时,动点的轨迹就是椭圆,而这个比值就是椭圆的离心率e=c/a。我们刚才从图中直观地看出“到两定点距离之和等于定长的点的轨迹是椭圆”,现在又从另一个角度即离心率的角度,仍然很直观地证明了截痕是椭圆。并且,这个新的定义更加方便我们今天后面所要讲的内容。
切割面的倾斜程度即φ唯一地决定椭圆的形状。切割面越倾斜,说明夹角φ越小,cosφ就越大。而cosφ就是离心率e,所以,截痕椭圆放平后就越扁。但是,因为不管截面如何倾斜,所截得的椭圆的短轴长度是不变的,都等于圆柱底面直径。
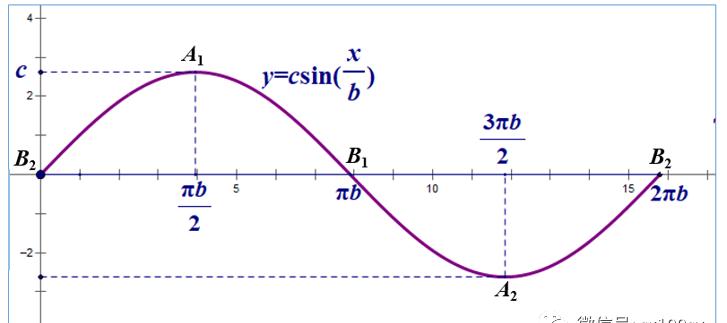
2. 下面我们研究圆柱的侧面展开图(展成平面)。展开后侧面外侧朝向我们的眼睛。我们若从过B1点的圆柱母线剪开圆柱,则椭圆正好变为正弦曲线,为正弦曲线的一个周期,这个周期为底面圆的周长2πr即2πb,所以角频率ω=1/b。所以,这个正弦曲线的方程中一定有sin(x/b)。然后我们来确定这个正弦函数的系数。

上图中,OA1=OA2=a,所以,观察直角三角形OA1D1,有A1D1:A1O=cosφ=e=c/a,所以,A1D1=c。所以,把圆柱侧面展开后,椭圆变来的正弦曲线的振幅就是c。椭圆上的点从B2开始逆时针旋转,经过A1、B1,A2,返回到B2,相应地,正弦曲线上的点B2就先从0上升到A1的c,再下降到B1的0,然后继续下降到A2的-c,从A2上升回到B2,完成一个周期的运动。从而,正弦曲线的方程就是
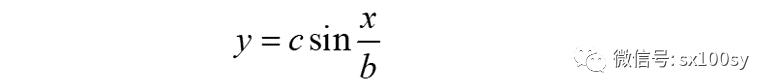
以上对平面切割圆柱得到椭圆的过程中涉及的相关知识进行了一些简单介绍。下面所讲是本篇内容一个更加深入且非常有趣的部分。
椭圆的周长一定等于正弦曲线一个周期的长度。下面我们通过微积分的方法,分别求出椭圆周长和正弦曲线一个周期的长度。你会发现,它们长度的表达式完全一样。
首先,我们把周长公式列在下面。对参数方程,周长公式为:
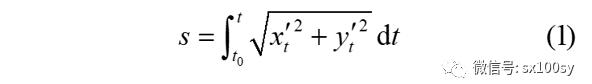
对直角坐标方程,周长公式为:
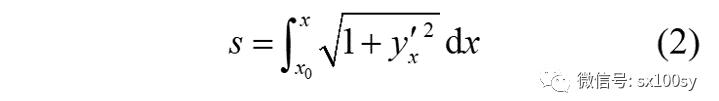
下面计算椭圆的周长。设椭圆的直角坐标方程为:
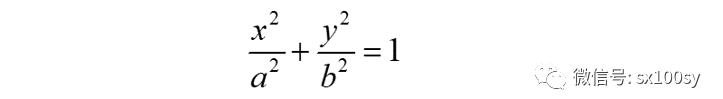
我们取y轴对应参数t=0,顺时针旋转为t增加的方向,则上面椭圆方程的参数方程为:
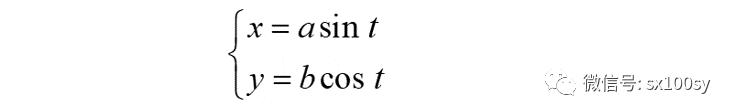
我们只需求四分之一即一个象限内椭圆孤长,再乘以4即可。根据曲线长度公式(1),得到椭圆的周长为:
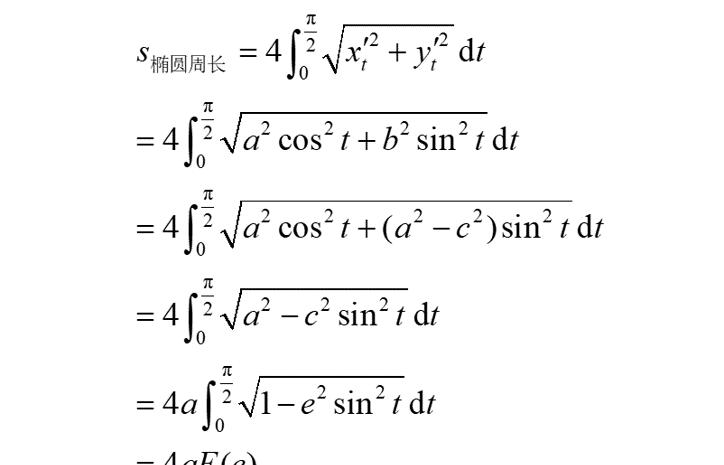
其中的E(e)是怎么回事,后面有说明。
再来计算正弦曲线一个周期的长度。正弦曲线的方程是
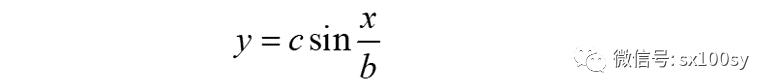
由曲线长度公式(2),得正弦曲线的长度为:
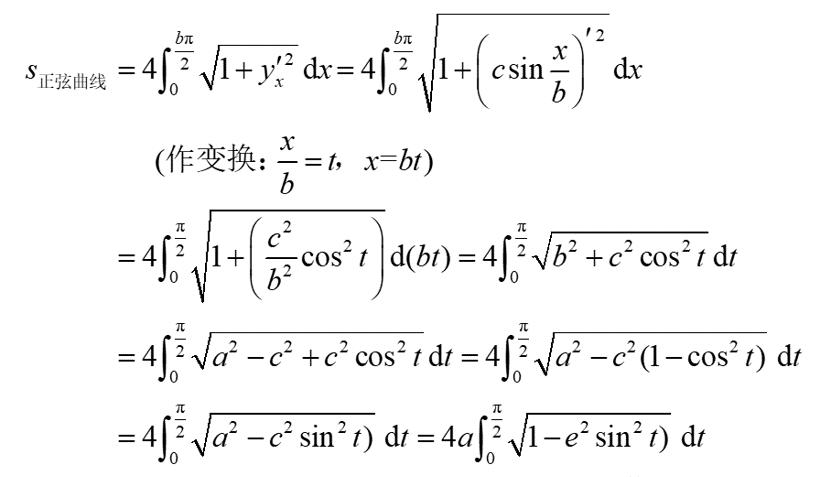
所以,

注意,上面用参数方程计算椭圆周长时,我们没有按照一般椭圆的参数形式,一般的参数形式是:
我们把sint和cost对调,是为了使得椭圆周长这个积分中,根号下出现的是有关sint的式子,而不是有关cost的式子。这样就与椭圆积分或勒让德积分联系了起来。第二类勒让德椭圆积分是:
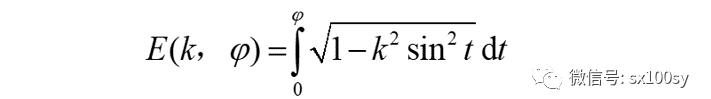
当φ为π/2时,第二类勒让德积分变为全积分:
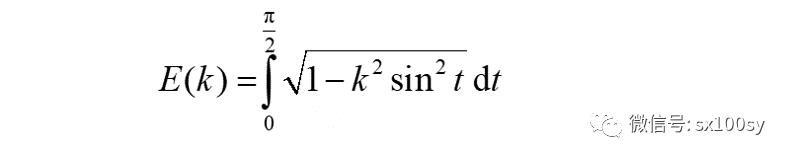
计算曲线(比如星形线,心脏线)的周长时会发现很多有趣的现象,以后会陆续介绍。
据说,在机械加工中,要用金属片弯曲成一个有斜截面的圆柱,就需要先画出并切出正弦曲线形状的边界。这个边界正是正弦曲线。两个这样做成的圆筒,在斜面处经过焊接,就成为弯管。几十年前家里生火把废气排到室外用的排气管,都会用到这样的接头。