Python数据结构与算法——第一课 什么是数据结构?
Python数据结构与算法——第二课 数据的逻辑结构
Python数据结构与算法——第三课 数据的存储结构/基本运算种类
Python数据结构与算法——第四课 俄罗斯套娃与递归
Python数据结构与算法——第五课 递归与循环
Python数据结构与算法——第六课 斐波那契数列
Python数据结构与算法——第七课 栈
Python数据结构与算法——第八课 汉诺塔
Python数据结构与算法——第九课 队列
Python数据结构与算法——第十课 单向链表节点操作算法
Python数据结构与算法——第十一课 单向链表操作之二
Python数据结构与算法——第十一课 单向链表操作之三
Python数据结构与算法——第十二课 单向链表操作之四
Python数据结构与算法——第十三课 单向链表操作之五
Python数据结构与算法——第十四课 单向循环链表与约瑟夫环
Python数据结构与算法——第十五课 双向链表
Python数据结构与算法——第十六课 双向循环链表
Python数据结构与算法——第十七课 数组的结构/重复元素/次大值
Python数据结构与算法——第十八课 数组支点/幸运值/二分法
Python数据结构与算法——第十九课 数组连续子串/过半数/环路加油站
Python数据结构与算法——第二十课 树结构/二叉树/插入/中序遍历
Python数据结构与算法——第二十一课 二叉排序树的深度优先遍历和广度优先遍历
Python数据结构与算法——第二十二课 二叉排序树的节点删除
Python数据结构与算法——第二十三课 二叉排序树按层遍历/深度/祖先
Python数据结构与算法——第二十四课 满二叉树
Python数据结构与算法——第二十五课 完全二叉树
Python数据结构与算法——第二十六课 平衡二叉树(AVL树)
Python数据结构与算法——第二十七课 平衡二叉树的节点删除
Python数据结构与算法——第二十八课 平衡二叉树的判定与转化
Python数据结构与算法——第二十九课 平衡二叉树的层数平衡法插入
Python数据结构与算法——第三十课 平衡二叉树的层数平衡法删除
Python数据结构与算法——第三十一课 平衡二叉树的层数平衡法转化
Python数据结构与算法——第三十二课 红黑树(RB-Tree)规则解析
Python数据结构与算法——第三十三课 红黑树的插入
Python数据结构与算法——第三十四课 红黑树的删除
Python数据结构与算法——第三十五课 红黑树的转化
Python数据结构与算法——第三十六课 堆结构/二叉堆的插入和遍历
Python数据结构与算法——第三十七课 二叉堆的删除
Python数据结构与算法——第三十八课 大(小)顶堆
Python数据结构与算法——第三十九课 大顶堆实现优先队列
Python数据结构与算法——第四十课 散列表(哈希表)
Python数据结构与算法——第四十一课 散列表(哈希表)的应用:除重/选票/交集
Python数据结构与算法——第四十二课 字典树添加与遍历
Python数据结构与算法——第四十三课 字典树的检索和节点删除
Python数据结构与算法——第四十四课 图
Python数据结构与算法——第四十五课 图结构的创建
Python数据结构与算法——第四十六课 图的遍历
假设需要在A、B、C、D、E五座城市间修建公路(五座城市间距离不同),如下示意图所示。
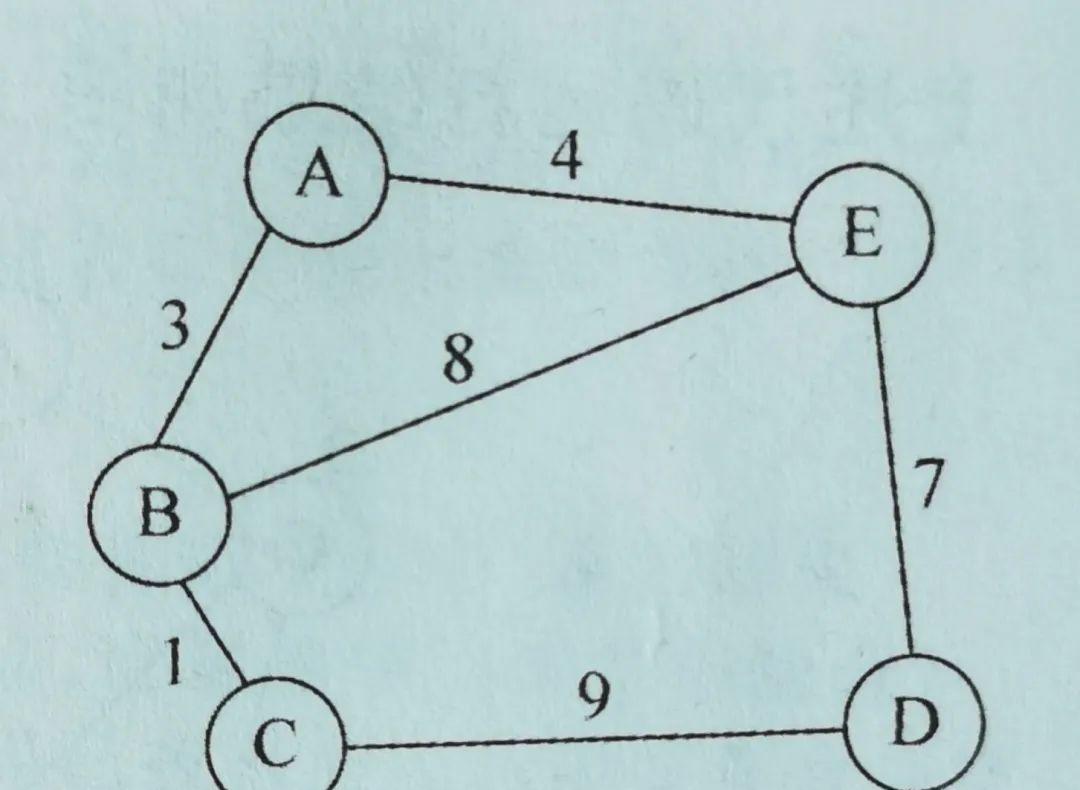
为节省资金,需要将公路修得尽可能短,但又要保证从任何一个城市可以到达另外一个城市。
首先我们讨论环路问题,像B到E,可以经过A再到达,B到E的直连就没必要。因此可以得出,方案中是不可以有环的。不带环的回路其实是一个树结构,此树称为生成树,如下图所示。

以上这些修路方案(生成树)肯定有一条路径是最短的,也就是最省钱的方案,这条权重和最小的方案(生成树)称为最小生成树。那么,如何用程序来找出这棵最小生成树呢?常用的算法有两种:Prim算法和Kruskal算法。下面以Prim算法为例求取上述最小生成树。
Prim算法是从图的一个初始顶点开始,寻找触达其他顶点权值最小的边,并把该顶点加入已触达顶点的集合中。当全部顶点都加入集合时,求最小生成树的工作就完成了。Prim算法的本质是基于贪心算法思想(不从全局考虑,把每一步做到最佳。可查阅百度。)。
本例中的最小生成树采用两个一维数组表示:一个一维数组负责存储已触达顶点;另一个负责存储每个已触达顶点对应的父顶点。求取最小生成树的算法图解如下图所示。


在实现Prim之前,显然需要图类(附录1到3)和最小生成树类(附录4)。
邻接矩阵有向实现代码(文本附录5):




运行结果:

邻接矩阵无向实现代码:
把

改为

运行结果:

邻接表有向实现代码(文本附录6):





运行结果:

邻接表无向实现代码:
把

改为

运行结果:

图的极小连接子图不能有回路(因为有回路就不是极小连接),而是一个树形结构,所以称为最小生成树,图的最小生成树不一定是唯一的,同一个图有可能对应多个最小生成树。
最小生成树在实际中的应用非常广泛,比如,城市间的光纤通信、铁路系统、水暖电气系统和路线选择等。
练习题1:修改上例的无向图Prim算法,使其返回全部起点的最小生成树,看看这些树是不是一样的?
练习题2:为何上例无向图的最小生成树与有向的不一样?
学思营编程课堂基于蓝桥STEM86平台https://www.stem86.com,开展学编程三部曲:
更多课程请打开“学思营”同步网站:
http://www.5xstar.com/doc.html
参考资料:
1、《Python算法图解》何韬编著 清华大学出版社
附录1:图结构.py

#图结构抽象类class Graph: #构造方法 def __init__(self, direct=False): self.direct = direct #是否有向 ”’图结构子类需要实现下面三种方法 #添加顶点 def addVertex(self,key): @key顶点的字符(键) pass #添加边 def addLine(self,start,ends): @start起点字符@终点[字符,权值]的列表 pass #打印 def display(self): pass”’
附录2:图结构_邻接矩阵.py



#创建带权重的图邻接矩阵from 图结构 import Graphclass GraphMatrix(Graph): def __init__(self, direct=False): Graph.__init__(self, direct) #调用超类构造函数 self.dict = {} #节点对应矩阵下标的字典 self.length = 0 #矩阵长宽,即节点数 self.matrix = [] #图邻接矩阵 #添加顶点 def addVertex(self,key): self.dict[key]=self.length #键(顶点名称): 值(矩阵中的长宽下标) self.dict[self.length]=key #键(矩阵中的长宽下标): 值(顶点名称) self.length = 1 #矩阵长宽加1 lst = [0 for i in range(self.length)] #创建一行长度为self.length的全0列表 self.matrix.append(lst) #向矩阵中添加全是0的一行 for i in range(self.length-1): #向已有的行添加添加一个0 self.matrix[i].append(0) #添加边 def addLine(self,start,ends): ”’@start起点字符@终点(字符+权值)数组@noDirect是否无向”’ startIndex = self.dict[start] #起点在二维矩阵中的下标 for row in ends: endKey = row[0] #另一节点值 endIndex = self.dict[endKey] #另一节点在二维矩阵中的下标 lineV = row[1] #起点到另一节点权值 self.matrix[startIndex][endIndex]=lineV if not self.direct: self.matrix[endIndex][startIndex]=lineV #打印矩阵 def display(self): lst = [self.dict[idx] for idx in range(self.length)] print(” \t” “\t”.join(lst)) for i in range(self.length): print(lst[i] “\t” “\t”.join([str(lineV) for lineV in self.matrix[i]]))#测试 激发《五行星学编程》使用idle运行 input()if __name__ == “__main__”: lst = [‘北京’,’天津’,’郑州’,’青岛’] start1 = ‘北京’ ends1 = [[‘天津’,138],[‘郑州’,689]] start2 = ‘天津’ ends2 = [[‘郑州’,700],[‘青岛’,597]] #与北京的连接已设置 start3 = ‘郑州’ ends3 = [[‘青岛’,725]] #与北京和天津的连接已设置 gMat = GraphMatrix() #创建一个空邻接矩阵 for city in lst: #加入顶点,创建全0矩阵 gMat.addVertex(city) gMat.addLine(start1,ends1) #加入以北京为起点的边 gMat.addLine(start2,ends2) #加入以天津为起点,不含北京的边 gMat.addLine(start3,ends3) #加入以郑州为起点,不含北京和天津的边 #打印矩阵 gMat.display()
附录3:图结构_邻接表.py



#邻接表方式创建图 from 图结构 import Graphclass GraphList(Graph): def __init__(self, direct=False): Graph.__init__(self, direct) #调用超类构造函数 self.dict = {} #顶点名为键,边链表为值,链表中存储其他节点的名称和权值 def addVertex(self,key): #添加新节点 self.dict[key]=[] #用列表代替链表 #添加边 def addLine(self,start,ends): ”’@start起点字符@终点(字符+权值)数组”’ for row in ends: key = row[0] #另一节点值 #在start的邻接表中追加新的边和权值 lst = self.dict[start] #start的邻接表 for kv in lst: if kv[0] == key: #如果链表中有这个主键,不进行添加 break else: #如果链表中有这个主键,进行添加(顶点名,权值)元组 self.dict[start].append(row) if not self.direct: #无向,在start顶点对应的邻接表中追加边和权值 lst = self.dict[key] for kv in lst: if kv[0] == start: break else: lst.append([start,row[1]]) #列表追加记录 #打印 def display(self): for key in self.dict: print(key,’=>’,self.dict[key])#测试 激发《五行星学编程》使用idle运行 input()if __name__ == “__main__”: lst = [‘北京’,’天津’,’郑州’,’青岛’] start1 = ‘北京’ ends1 = [[‘天津’,138],[‘郑州’,689]] start2 = ‘天津’ ends2 = [[‘郑州’,700],[‘青岛’,597]] #与北京的连接已设置 start3 = ‘郑州’ ends3 = [[‘青岛’,725]] #与北京和天津的连接已设置 gList = GraphList(True) #创建空邻接表 for city in lst: #添加顶点,每个顶点有一个空列表 gList.addVertex(city) gList.addLine(start1,ends1) #加入以北京为起点的边 gList.addLine(start2,ends2) #加入以天津为起点,不含北京的边 gList.addLine(start3,ends3) #加入以郑州为起点,不含北京和天津的边 #打印邻接表 gList.display()
附录4:最小生成树.py



#最小生成树#最小生成树节点类class MGTNode: def __init__(self, key=None, value=None): ”’@key顶点键@value权值”’ self.key = key self.value = value self.pointers = [] #子节点指针集合#最小生成树类class MinGraphTree: def __init__(self, reachedVertexList, parents): ”’@reachedVertexList触达(顶点键,权值)顺序列表@parents父顶点键列表”’ self.length = len(reachedVertexList) #树的节点数 (key0, value0) = reachedVertexList[0] #解包根顶点 self.root = MGTNode(key0, value0) #数的根节点 ps = {key0 : self.root} #顶点键与节点字典 for i in range(1, self.length): #填充树节点 (key, value) = reachedVertexList[i] #顶点键 parentKey = parents[i] #顶点父顶点键 parent = ps[parentKey] #顶点父节点 node = MGTNode(key,value) #节点 ps[key] = node #加顶点入字典 parent.pointers.append(node) #把节点加入树中 def display(self): #遍历 self.__display(self.root, “”, 0) def __display(self, node, path, sumValue): #递归遍历 ”’@node当前节点@path路径@sumValue权值和”’ path = “-” node.key sumValue = node.value print(“路径:”, path, “权值合计:”, sumValue) #打印上级节点 if len(node.pointers) > 0: #下级指针集合中有记录 lst = node.pointers #获取下级集合 dlen = len(lst) print(“序号\t键\t值\t下级集合”) for i in range(dlen): nd = lst[i] dw = “有” if len(nd.pointers) > 0 else “无” #是否有下级集合 print(“%d\t%s\t%s\t%s” % (i, nd.key,str(nd.value),dw)) #打印一行 dnum = input(“请输入下级序号:”) if dnum != None and dnum != “”: dnum = int(dnum) if dnum>-1 and dnum < dlen: self.__display(lst[dnum], path, sumValue) #测试if __name__ == “__main__”: __lst = [(‘A’,0),(‘B’,3),(‘C’,1),(‘E’,4),(‘D’,7)] __ps = [None, ‘A’, ‘B’, ‘A’, ‘E’] __tree = MinGraphTree(__lst,__ps) __tree.display()
附录5:邻接矩阵Prim.py
#邻接矩阵Prim最小生成树from 最小生成树 import MinGraphTreefrom 图结构_邻接矩阵 import GraphMatrix#Prim算法def matrixPrim(gMat): ”’@gMat邻接矩阵图”’ result = None for index in range(gMat.length): #从0开始扫描起点 reachedVertexList, parents, sumValue = __matrixPrim(gMat, index) #尝试一次 if reachedVertexList != None: #找到一个解决方案 print(index,reachedVertexList, parents, sumValue) #测试 if result == None or sumValue < result[2]: result = (reachedVertexList, parents, sumValue) if result == None: return None else: return MinGraphTree(result[0],result[1])def __matrixPrim(gMat, index): #尝试index开始的最小树 reachedVertexList = [index] #已加的索引 parents = [None] #父顶点索引 values = [0] #权值 __matrixPrimRecursion(gMat, reachedVertexList, parents, values) #递归计算 if len(reachedVertexList) == gMat.length: #最小树生成成功 for i in range(gMat.length): #转换触达表 reachedVertexList[i] = (gMat.dict[reachedVertexList[i]],values[i]) for i in range(1,gMat.length): #转换parents, 第0个不用转换 parents[i] = gMat.dict[parents[i]] return reachedVertexList, parents, sum(values) #返回方案 else: return None,None,None def __matrixPrimRecursion(gMat, reachedVertexList, parents, values): minWeight = 0 #最小权重值 minIndex = None #最小权重值对应的节点 pIndex = None #最小权重值对应的节点的父节点 for rindex in reachedVertexList: #遍历已触达顶点列表 for i in range(gMat.length): #横向扫描矩阵 if i in reachedVertexList: #跳过已触达顶点 continue v = gMat.matrix[rindex][i] #获取已触达顶点到此顶点的权值 if v>0 and (minWeight==0 or minWeight>v): #有连接并且是第一个或比最小值小 minWeight = v minIndex = i pIndex = rindex #最小权值对应的父节点 if minIndex!=None: #找到最小出路 reachedVertexList.append(minIndex) #把最小权值边对应的顶点放入已触达顶点集 parents.append(pIndex) #把新的已触达顶点的父顶点的下标放入parents values.append(minWeight) #把新的已触达顶点的权值加入 __matrixPrimRecursion(gMat, reachedVertexList, parents, values) #递归找下级#测试 激发《五行星学编程》使用idle运行 input()if __name__ == “__main__”: lst = [‘A’,’B’,’C’,’D’,’E’] lstA = [[‘B’,3],[‘E’,4]] #A连接B、E lstB = [[‘C’,1],[‘E’,8]] #B连接C、E lstC = [[‘D’,9]] #C连接D lstD = [[‘E’,7]] #D连接E gMat = GraphMatrix(True) for key in lst: gMat.addVertex(key) gMat.addLine(lst[0],lstA) gMat.addLine(lst[1],lstB) gMat.addLine(lst[2],lstC) gMat.addLine(lst[3],lstD) gMat.display() print(‘————————‘) mgTree = matrixPrim(gMat) #转为最小生成树 if mgTree != None: mgTree.display()
附录6:邻接表Prim.py
#邻接表Prim最小生成树from 最小生成树 import MinGraphTreefrom 图结构_邻接表 import GraphList#Prim算法def listPrim(gList): ”’@gList邻接表”’ result = None for startKey in gList.dict: #扫描所有键作为起点 if len(gList.dict[startKey]) == 0: #跳过无连接出的顶点 continue reachedVertexList, parents, sumValue = __listPrim(gList, startKey) #尝试一次 if reachedVertexList != None: #找到一个解决方案 print(startKey,reachedVertexList, parents, sumValue) #测试 if result == None or sumValue < result[2]: result = (reachedVertexList, parents, sumValue) if result == None: return None else: return MinGraphTree(result[0],result[1])def __listPrim(gList, startKey): #尝试startKey开始的最小树 reachedVertexList = [startKey] #已加的索引 parents = [None] #父顶点索引 values = [0] #权值 __listPrimRecursion(gList, reachedVertexList, parents, values) #递归计算 length = len(gList.dict) #顶点数 if len(reachedVertexList) == length: #最小树生成成功 for i in range(length): #转换触达表 reachedVertexList[i] = (reachedVertexList[i],values[i]) return reachedVertexList, parents, sum(values) #返回方案 else: return None,None,None def __listPrimRecursion(gList, reachedVertexList, parents, values): minWeight = 0 #最小权重值 minKey = None #最小权重值对应的节点 pKey = None #最小权重值对应的节点的父节点 for rKey in reachedVertexList: #遍历已触达顶点列表 row = gList.dict[rKey] #获取键的行 if len(row) == 0: #跳过无连出的顶点 continue for [otherKey, v] in row: #扫描行,获取已触达顶点到此顶点的权值 if otherKey not in reachedVertexList and \ (minWeight == 0 or minWeight>v): #未触达有连接并且是第一个或比最小值小 minWeight = v minKey = otherKey pKey = rKey #最小权值对应的父节点 if minKey!=None: #找到最小出路 reachedVertexList.append(minKey) #把最小权值边对应的顶点放入已触达顶点集 parents.append(pKey) #把新的已触达顶点的父顶点的下标放入parents values.append(minWeight) #把新的已触达顶点的权值加入 __listPrimRecursion(gList, reachedVertexList, parents, values) #递归找下级#测试 激发《五行星学编程》使用idle运行 input()if __name__ == “__main__”: lst = [‘A’,’B’,’C’,’D’,’E’] lstA = [[‘B’,3],[‘E’,4]] #A连接B、E lstB = [[‘C’,1],[‘E’,8]] #B连接C、E lstC = [[‘D’,9]] #C连接D lstD = [[‘E’,7]] #D连接E gList = GraphList(True) for key in lst: gList.addVertex(key) gList.addLine(lst[0],lstA) gList.addLine(lst[1],lstB) gList.addLine(lst[2],lstC) gList.addLine(lst[3],lstD) gList.display() print(‘————————‘) mgTree = listPrim(gList) #转为最小生成树 if mgTree != None: mgTree.display()