1.向你介绍我是谁

大家好!我是邓招徒,来自杭州市天长小学,是朱乐平名师工作站的成员,很高兴能在“一课研究”平台与您相遇!
2.本期内容有哪些
(1)听一听:机械学习孰好孰坏
(2)读一读:发现规律背后的本质知识
——“循环小数”教学实践与思考
(3)思一思:百分率陷阱


3.轻轻松松听听书
我们知道,数学学习需要学生记忆并能回忆大量的基础知识,比如加法算式,乘法表,运算法则,所以它极易受机械学习的影响,然而,从长远看,机械学习并不能达到所期望的准确回忆和反应的目的。
4.坚持阅读8分钟

发现规律背后的本质知识
——“循环小数”教学实践与思考
【教学内容简析】
在以往的教学中,常通过观察除法计算结果,使学生明白商的结果分有限和无限情况,明晰循环小数的概念,会记录和读写循环小数。老师们比较注重规律的观察和概念的揭示,然后练习,扎实掌握技能,也就是从“象”的揭示到“术”的应用方面做得比较足,可是学生对于“象”背后的“理”能否进一步理解呢?
我们希望通过观察除法竖式过程,使学生知道不同余数出现次数和小数循环节位数是一致的;通过说理辨析活动,使学生理解除法的非整数商只有有限和无限循环结果,并能迁移理解到小数除法的一致性;重点是理解循环节位数和除数大小关系。
本课安排了两个大环节给学生探究发现:一是研究为什么会出现循环,和什么有关;二是循环节的位数和出现不同的余数次数有什么关系。
【教学实施】
一、前测题引入,讨论商的结果并分类。
1.出示习题,学生观察。
师:课前老师给你们做了几道除法计算的题目,今天我们就一起来研究这些除法算式。请看,这些除法算式有什么共同特点?(都是整数÷整数,结果都是小数)
1÷2= 1÷3= 1÷6= 5÷4= 29÷22= 16÷99=
(1)出示题目作品。
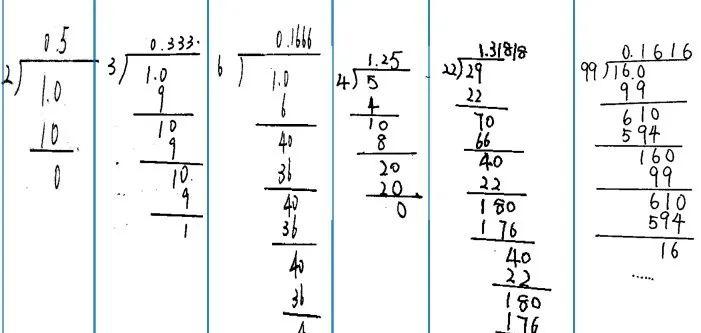
(2)我也收集了几个作品,一起来看一下。你能根据商的结果来分分类吗?
(3)哪里看出除尽了。
(4)你们知道能除尽的叫什么小数,不能除尽的叫什么小数吗?
(5)分得非常清楚,接下来我们来研究这种除不尽的情况。
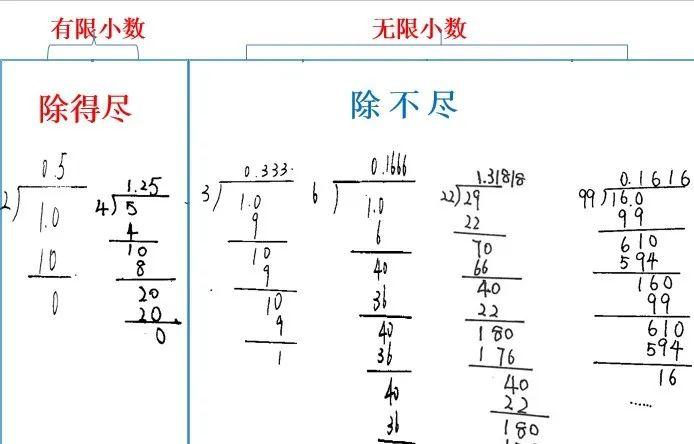
[设计意图]:通过课前调查,发现很多孩子已经知道无限小数的意思,所以把计算提到课前进行,能够留出更多的时间给孩子观察分类,分类能让学生明晰思维,进而能有更多时间来让学生研究除不尽的现象。

二、教学循环小数概念。
1.探讨商的特点和背后原因。
(1)小组研究活动1:
观察商的特点,尝试解释有这样的特点的原因;找到原因的可以在竖式上表示出来。
(2)教师来回巡视,指名汇报特点。
(3)汇报特点。师:同学们合作探索和交流地都很好,请代表说一说商的特点,把观察到的说出来。
生:商不断重复出现,商循环了。(板书:重复出现)
追问:你说的重复出现指的是什么?循环什么意思?能说一说哪些数字重复出现了?
追问:重复出现是只能重复2次或者3次吗?(板书:不断)
(4)师:这4个商的小数部分都有不断重复出现的现象,有什么不同的地方吗?
生:有的是从十分位开始就重复,有的是从百分位开始重复,有的是1个数字在重复,有的是2个数字在重复。
评价:同学们发现了问题(板书:发现问题),能去认真观察,这是很棒的学习方法。
[设计意图]:学生观察现象,老师把学生的方法提炼出来并板书,提升学生发现问题的能力。
2.揭示循环小数概念。
(1)你知道像这样的小数叫什么小数吗?
(2)出示概念:一个小数,从小数部分的某一位起,一个数字或者几个数字依次不断重复出现,这样的小数就叫循环小数。依次不断重复出现的数字,叫做这个循环小数的循环节。
3.循环小数的简便写法和读法。
(1)师:你能说一说这些循环小数的循环节吗?
(2)怎么去表示循环小数呢?(板书:解决问题)教师出示学生的记录方式,说一说表达的意思。
(3)对比:你更喜欢哪一种?为什么?
(4)出示错例,丰富认识概念内涵:你觉得这样可以吗?质疑。
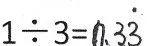
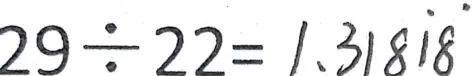
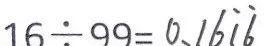
4. 探索小数部分不断重复出现的原因。
(1)我们知道了循环小数,知道了循环小数有不断重复现象,谁来汇报为什么会出现循环?(板书:探寻原因)
(2)反馈。
生1:1÷3,余数1的时候,就商3,余数一直是1,商就一直是3.
生2:1÷6,当余数出现4的时候,商就是6,一直重复。
生3:29÷22,余数出现4,商是1,余数出现18,商是8,一直重复下去。
(3)师:也就是说重复的余数出现了,商也会有规律地重复出现。有什么补充吗?
(4)跟进基本练习1,认识循环节的唯一性。
23÷54= 4÷13=

三、深入探讨、理解本质知识。
1.环节小结,引发探讨:刚才我们谈论的整数÷整数的除法算式结果中,如果除不尽的话,就会出现循环小数,有没有可能是无限不循环的?你能猜猜看吗?
2.形成猜想:认为可能的人,怎么办(验证)。不可能的人怎么办,举一个反例。老师也给每个小组准备了一道题,我们来验证一下吧。
3.每个小组做一道题试一试。
小组研究活动2:
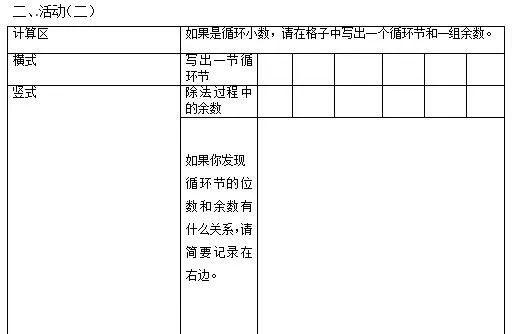
(1)2÷11= (2)8÷11= (3)1÷7= (4)3÷7=
(5)27÷101= (6)23÷27= (7)4÷9= (8)7÷9=
(1)每一小组选择自己组号的一道题计算,并写出答案。
(2)如果是循环小数,请在格子中写出一个循环节和一组余数。
(3)猜一猜循环节的位数和余数的出现有什么关系。
附:学习单。
4.校对。
(1)指名回答,教师灯片打出。
(2)这里8道除不尽的算式,商都是循环小数,现在认为可能的同学们,是不是有点信心了啊,如果再举多一些可能会更有感觉。我们把余数也填进去,说一说发现什么?
(板书:余数出现几次,循环节位数就几位)
(3)重点以除数是7为例。
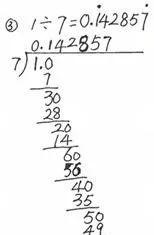
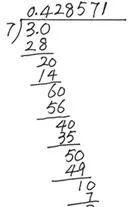
提问:那余数可能出现7吗?为什么?(板书:余数比除数小)
(4)连起来怎么说,(板书:余数<除数,重复的余数个数=循环节位数,循环节位数<除数)
(5)质疑:有人在做5÷7时,结果写成了0.7142856,7142856循环,你能判断他是错的吗?
生:因为不同余数的数量总是比除数小1,所以循环节的位数最多最多也是比除数小1。
[设计意图]:通过分组探讨,让学生理清循环节的位数和不同余数的出现次数是一致的,而余数总是会比除数小的,所以不可能出现不同余数个数和除数相等情况,并让学生通过这一发现,解决问题。
5.深入思考:循环节的位数和余数的关系以及商的特点。
(1)讨论:1÷17你觉得循环节最多有多少位?
(2)思考:1÷17的循环节可能是17位吗?为什么?(余数次数和循环节位数相同,都要比除数小)
(3)呈现竖式并质疑:在这个循环节中为什么商有出现相同的数,比如有2个8,他们是同样的余数补0除得的吗?
(4)猜猜看:1÷23=的循环节位数呢?(22位)
(5)继续猜:1÷1861(1860位),1÷17938(17938位)
师:此刻你有什么想法想表达?
猜想:现在你觉得两个整数相除会不会得到不循环小数呢?为什么?
(6)再猜一个:1÷123的循环节位数?(为什么不是122位了,而是5位呢?)
[设计意图]:学生在研究循环节位数和除数关系时,往往会有一个认知的迷失点,就是余数重复出现和商部分的数字重复出现会搞混。
比如1÷17=0.0588235294117647…,这里要让学生明白,在一个循环节中,商的数字可能会有一样的。但是一样的商,却是不一样的余数补0后除出来的结果,比如上面的千分位和万分位的8,分别是150和140除以17的结果,继而要让学生认清的理是:余数如果重复出现了,那么商的循环才会开始。
通过大数据的表达,让学生逐步相信,如果除不尽,那么循环节的位数个数范围总是可以确定的,但是这样立起来的认知,需要用类似1÷123这样的除式来破一下,从而完善认知。

四、课堂总结、延伸。
师:这节课我们研究了什么?
师:如果是小数除以小数,除不尽的话,商也一定是循环小数吗?其实还有更多内容等着大家去研究,有兴趣的可以课外再去研究研究,也可以把研究成果和你们的小伙伴或者是老师分享。
5.思一思:百分率陷阱
医药研究者在实验一种新药,据称能改进人的智力。博士首先对他的一组病人进行试验,作为优秀的科学家,他决定给予一些病人真正的新药,而其余病人以“安慰剂”(不含药物的药片)。他的结果如下:
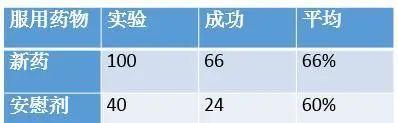
博士认为新药比安慰剂更有效,但是因为结果很相近,博士决定对更大的病人组重复这个实验。结果令人鼓舞,请看下面这组数据,博士认为服用新药的病人的表现又一次胜过服用安慰剂的病人。
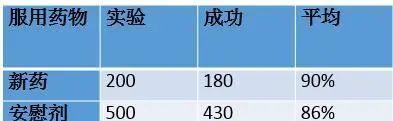
医药公司老总对这个发现很是兴奋,决定把他们的数据合并起来公布结果,但是使它们困惑的是看到了最意想不到的结局,尽管在两项实验中新药都比安慰剂成功,但是将两项测验合并起来时,服用安慰剂的病人竟然比新药更成功。
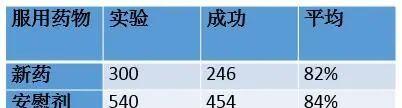
这个结果太使人惊奇了,以致科学家把它看成视错觉的数学等价物,朋友们,你们看出问题了吗?
是的,如果认为百分率可以像简单数字一样地合并的逻辑,那就大错特错了,百分率是不能相加求平均的,就像速度不能用这种方法取平均一样。