统计学（statistics）是一门收集、处理、分析、解释数据并从数据中得出结论的科学。统计的一般过程分为：统计设计->收集资料->整理资料->分析资料->得出结论。
可以说，统计学无处不在。日常购物货比三家；家庭理财比较收益；孩子考试成绩对比分析……就连斗地主，打麻将等游戏都存在统计学的身影。可是学习统计学是一件让你很头疼的事，各种概念，各种公式，可是为什么我们还执意要学呢？那还不是因为：
今天，给大家总结一下统计学中的几个入门级公式。
1平均数
M=(X1 X2 … Xn)/n （主要用于未分组的原始数据）
思考题：马云一天挣2个亿，马化腾一天挣1个亿，你一天挣500，请问你们3人一天平均收入是多少？
2中数
定义：中数（又名中位数，符号为Md）是按顺序排列在一起的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比它大，有一半的数据比它小。计算方法：如果数据个数是奇数，则中数为(N 1)/2，如果数据个数为偶数，则中数为居于中间位置两个数的平均数。
【测验1】有2，3，5，7，8，19，15，19共计8个数，求其中数。
第4个数是7，第5个数是8，故Md=(7 8)/2=7.5
【敲黑板时间到：考试题】当重复数位于数列中间
3众数
众数（mode）是在一组数据中,出现次数最多的数据，是一组数据中的原数据，而不是相应的次数。符号：Mo
【测验2】在偏态分布中，平均数、中数、众数三者之间的关系()。A．M=Md=Mo B．Mo=3Md-2MC．M＞Md＞Mo D．M＜Md＜Mo正式答案：B画重点：皮尔逊经验公式：（M-Md)/(M-Mo)=1/34百分位差
如果将一组数据从小到大排序，并计算相应的累计百分位，则某一百分位所对应数据的值就称为这一百分位的百分位数。可表示为：一组n个观测值按数值大小排列。如，处于p%位置的值称第p百分位数。举例：如P75=90，实际是指在这组数据中90分以下的数据包含了整个数据的75%。百分位差：P90-P10。学了这个到底有什么卵用？
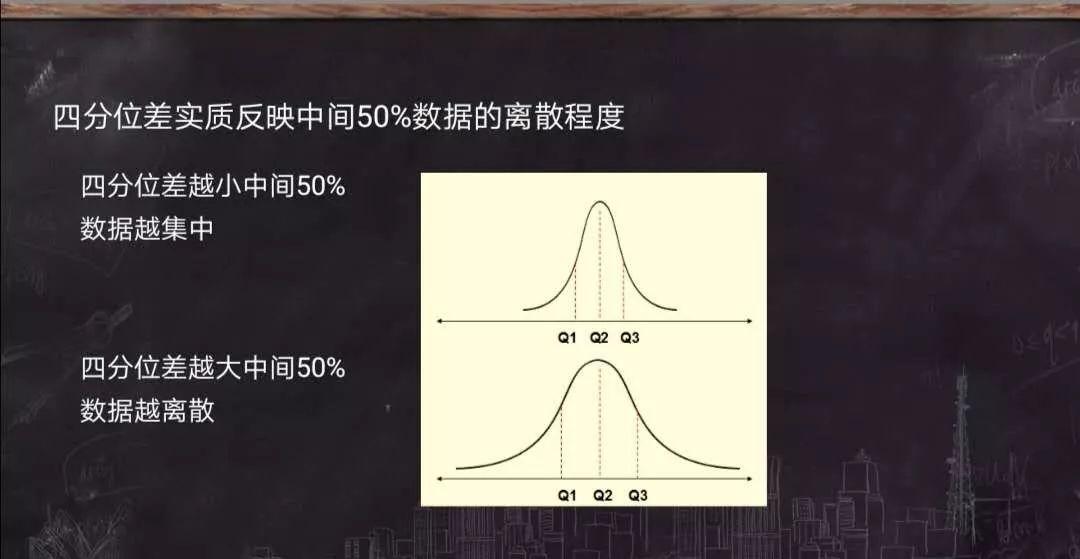
【提问】请问你家的孩子身高和体重是在标准范围内吗？请先看下面两张图
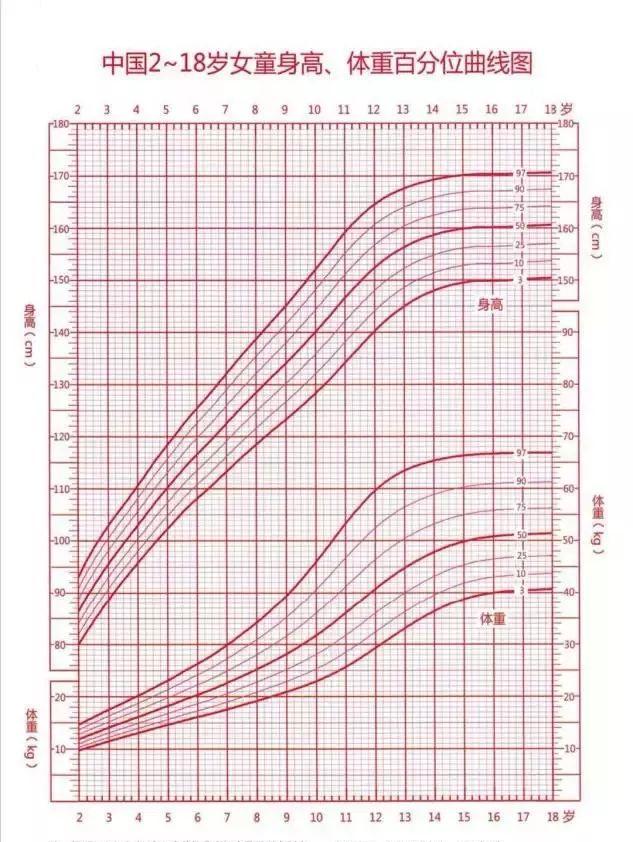
四分位数可理解为百分位数的特例，用Q来表示。P25，P50，P75把数据分成四等分，所以称为四分位数。四分位差：(P75-P25)/2=(Q3-Q1)/2实质：反映了中间50%数据的离散程度。
6方差
定义：统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。
7标准差
定义：标准差是方差的算术平方根。标准差是一种表示分散程度的统计观念。标准差已广泛运用在股票以及共同基金投资风险的衡量上，主要是根据基金净值于一段时间内波动的情况计算而来的。一般而言，标准差愈大，表示净值的涨跌较剧烈，风险程度也较大。
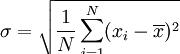
标准差在日常生活中又有哪些应用呢？举个例子，班上张三和李四两个同学，一学期8个单元考下来平均分都是80分，详细成绩如下表：
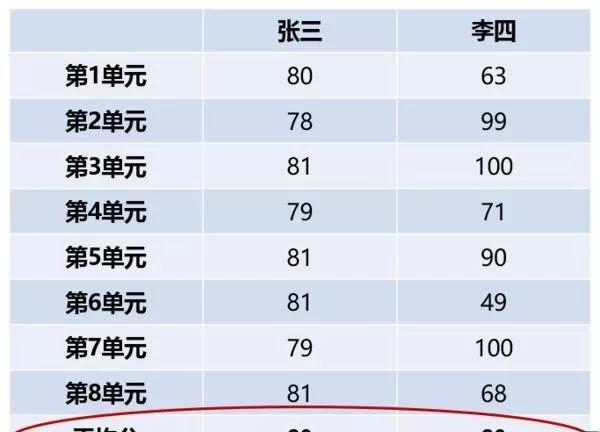两个同学的成绩，通俗的说就是张三成绩很稳定，李四波动很大。如果为了提高逼格，可以用今天要讨论的专业术语表述：李四的成绩标准差比张三大。根据计算张三的标准差是1.12，李四的标准差是18.49。怎么样，以上公式你掌握了多少呢？今天先告一段落吧，估计大家看到这里也快迷糊了。下一篇难度指数升级！
以上公式来自《现代心理与教育统计学》这本教材，是我整理的中科院心理所研修班的课后笔记，欢迎大家评论、
▼ 阅读，分享，成长▼
学习宝座请上座
