matlab曲线拟合函数有哪些(常用的曲线拟合函数)-众学网

写在前面的话：

大家好！我是凯森赛。常年从事地理研究，新人网络写手。先谈下本文的写作初衷，并不是为了营销，就是想借用【数读城事】这个平台练习一下科研教学与写作，并实实在在地传授一些速成学习法和笔者自己体会的科研心得。或许在某些细节上还没有照顾到所有读者，亦或许笔者在语言上并没有表达到位，也可能会有些疏漏或谬误，但如果可以在留言区跟读者朋友互动的话，笔者会很欣慰，同时笔者也会继续磨练写作技术的，非常感谢您的支持！各位的支持就是我前进的动力！在科研的旅途上，你并不是一个人！

特别声明：本文所有图片均由笔者的电脑所安装的MATLAB生成。所用MATLAB版本或者文中图片可能存在不一致或语言系统混乱的情况，这是因为笔者在学生时代曾经更换过电脑，望读者朋友谅解。所用的数据均注明了出处，请勿产生版权纠纷。配套教材的话，笔者推荐由北京大学陈彦光老师所著的《基于Matlab的地理数据分析》（高等教育出版社），有兴趣的朋友可以自行购买。深度阅读本文需要约30-40分钟，并要求一定的数学和地理学知识，具体可以查阅互联网或相关书籍，本文仅在个人立场给出解释，其余方面不多做赘述，望谅解。另外，Excel上绘制散点图之后也可以快速进行曲线拟合并给出拟合优度R2，回归系数或截距等参数，但是Excel在这里并不能给出统计学检验，并且并不是很User-friendly，加之基于Excel的统计学分析则需要添加Data Analysis的插件才可以，另外SPSS其实也可以胜任各类统计学分析，但SPSS需要比较详尽的设定才能run出比较合适的结果，并且它无法像MATLAB这样可以做到一步步运算并让用户体会到计算思路。MATLAB在数据量很庞大的时候，运算速度也远胜于SPSS与Excel。感兴趣的朋友可以进行其他的尝试，在此笔者就不做赘述。

【入门篇】

如图1所示：

①工作空间workspace。能够显示当前工程内被input的变量，并给出了各个变量的name，size等信息。比如图所示的A就是一个3×3的二维矩阵。利用MATLAB的save函数可以将工作空间所有的数据储存到mat文件中。

②命令履历表。可以拖曳到命令窗口③之中，也双击再次运行同样的命令。多行选中之后还可以另存为m文件保存成DIY的脚本。

③命令窗口。顾名思义就是敲command的地方了。

④菜单和快捷按钮。功能与小技巧很多，在此就不多做介绍。初学者可以在命令窗口输入help命令，给出帮助列表。也可以查询特定的帮助信息，比如输入命令help regress即可获得此函数的所有帮助信息。另外还有demo命令，demo命令可以调出实例演示，也可以单击菜单中的帮助列表查询详细的帮助信息的manual，亦可以通过网络搜索MATLAB官方网站或论坛查找相关知识，在此不赘述。

⑤文件夹目录。建议选择一个非C盘符下清晰明确的新建文件夹的路径。新建文件夹作为工程路径，这一点对于对于数据的管理，m文件的运行，save，load等函数的运行以及大型脚本的运作都至关重要，有兴趣的朋友可以进一步学习，此文暂时不谈。

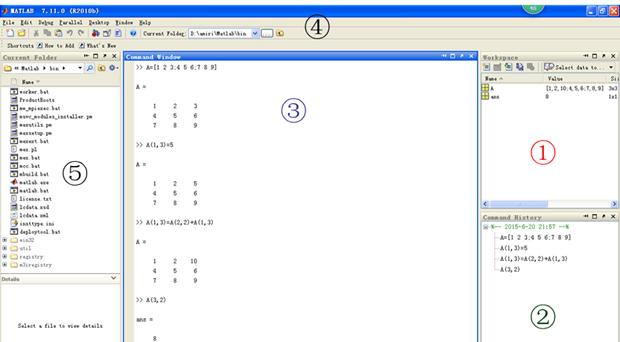图1

MATLAB的基本操作

接下来介绍MATLAB的基本操作。在命令窗口的>>符号后面输入command，按Enter键即可依据指令运行命令。例如图2所示的四则运算，图3所示的算数平方根，绝对值，幂函数以及对数函数的运算。这里需要特别指出一下，ans表示当前命令的返回值。如果给变量赋值，需要输入等号，比如a=1 1。command后面加上分号的话，比如a=1 1;则不会返回结果，仅在workspace出现变量a，不会在command窗口显示结果，只需输入a再敲Enter键即可返回a=2。

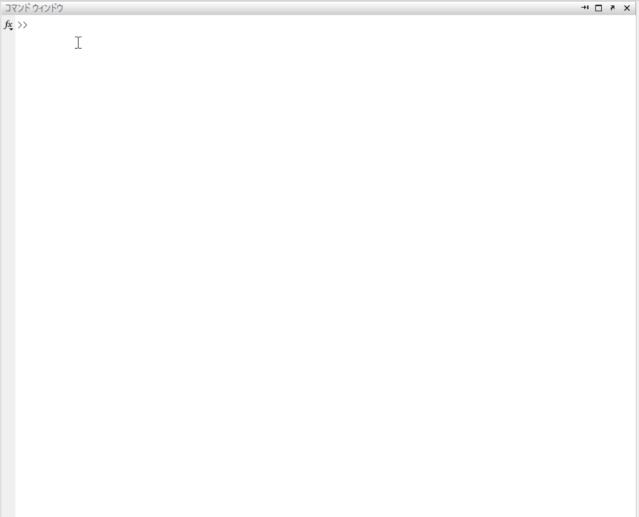
图2

图3

为什么要做曲线拟合？

这里简单说一下笔者的见解。所谓的曲线拟合，就是使用某一个模型（比如一元线性模型、指数模型以及Logistic模型等），将一系列的数据拟合成平滑的曲线，以便观察两组数据之间的内在联系，了解数据之间的变化趋势。曲线拟合在科学研究、数学建模、实验分析以及程序开发上都有很大的用处。这里谈到的曲线拟合，可根据自己的需要，选择不同的模型，可得出不同的效果。很多情况下，我们都需要采用非线性的模型去模拟与定量数据之间的数理关系，并通过解释回归系数、截距或者相关参数来掌握模拟系统的情况，进而通过曲线拟合对数据内涵进行可视化解读。在地理界的学术论文中，曲线拟合之后的解释与分析也是必不可少的。

【实例1】一元线性回归分析模型拟合

[B,Bint,E,Eint,Stats]=regression[Y,X,a]

X表示自变量的观测值（列向量形式，常数项需要加入一列ones矩阵）。Y为因变量的观测值（列向量）。A为显著性水平，可缺省，默认值为a=0.05。B为回归系数的最小二乘估计向量，一元线性回归模型中的即为y=ax b的截距和斜率；Bint为回归系数的（1-a）百分比水平的区间估计；E为残差向量；Eint为残差向量的区间估计；Stats则返回R2统计量，F统计量，F统计量对应的概率值（sig）和均方差（MSE）。关于模型的各类指标与统计学检验将在下文介绍。计算程序的m文件在图4（原始数据显示不完全）中给出，事先应该将房价数据的Excel文件存入指定的文件夹路径（folder path）以方便读取，实例训练中宜直接采用拖曳的方式（也可以复制粘贴再加上中括号的方式）导入原始数据（因为x，y变量需要事先指定规格）。存储代码MATLAB的m文件已存入本次的百度云分享链接，但希望好孩子可以不要嫌麻烦，认真按步骤手动敲代码体会过程，哈哈。

接下来对m文件的代码进行逐行解释：

第2行：clear是清空目前workspace的所有内容。第3-4行：加载x与y的原始数据（可以复制粘贴）。第5行：对x和y进行底数为e的对数变换。第6行：创造第一个图形。第7行：绘制散点图，yvs.x，红色的圈。第8-9行：添加坐标轴标签。第10行：保持图形。第11行：计算自变量矩阵行列数。第12行：在自变量矩阵中添加常数向量并转置。第13行：因变量矩阵转置。第14行：调用线性回归程序。第15行：自变量重新排序。第16行：模型建设。第17行：添加趋势线。第18行：计算预测值置信尺度。第19行：计算预测值的上下限。第20行：保持图形。第21行：将上限值的趋势线添加到图形中。第22-23行：将下限值的趋势线添加到图形中。第24行：绘图结束（第一个图形之中）。第25行：计算标准误差RMSE。第26行：创造第二个图形。第27行：绘制残差变化区间图。第28行：显示主要结果。

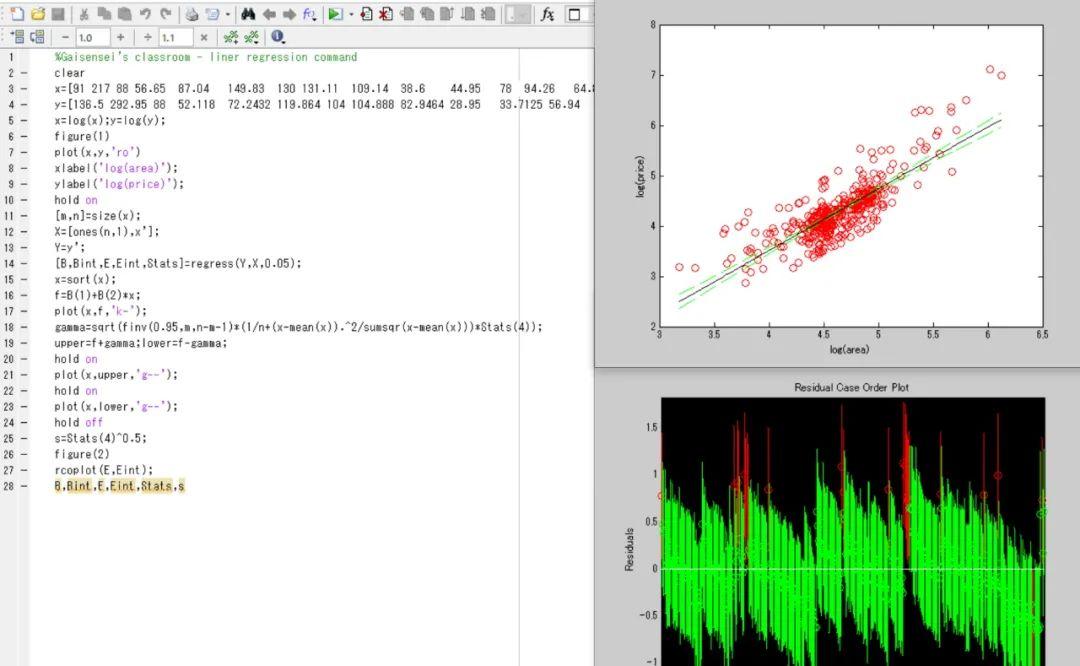图4??

关键指标解释

B=[-1.4079;1.2295]表示回归模型可以写作y=-1.4079 1.2295x；MATLAB默认显示小数点四位。Bint为回归系数的（1-a）百分比水平的区间估计；E为残差向量；Eint为残差向量的区间估计。

统计学检验指标

对于一元线性回归分析而言，F检验，T检验和相关系数检验是完全等价的。R??为回归模型的决定系数，也可以理解为拟合优度（全局拟合效果的好坏），一般超过0.6则视为拟合较好（很多研究中都不一定要强求）。

在本例中，输入Stats（1）即可给出R??=0.6556。F统计量为715.6897,Fsig=0.0000对于一元线性回归sig值与弃真概率P值相等，输入sig=Stats（3）即可得到sig的精确值4.7622e-089。综上所述，本例中得到的一元线性回归模型检验合格，在99%的水平上显著。??

残差分析

这个在计量地理学之中很常见，可以通过找到异常值来确认哪些样本有较大的残差，进而推测整个回归系统有哪些未考虑的因素未被考虑或者在某些特定区域存在某些特征。

从右下图的残差变化区间图可以看出某些样本是红色的，具有较高的残差。这说明这些样本都是过小估计的情况，也就是说一元线性回归模型所计算的预测值较观测值（真值）偏小。这就意味着这些样本在除了面积之外还有其余因素（比如区位）造成了更高的溢价。经过检查，我们不难发现造成正数残差的样本大多分布在西安市曲江池别墅区、高新技术开发区、大学城以及未央经济开发区。建议有兴趣的读者朋友参考Liu & Ichinose (2017)这篇论文中进行的基于SPSS的Hedonic回归分析以及残差分析，在此就不多做赘述。

【实例2】帕累托距离衰减模型的拟合

自然要素和社会经济要素的分布具有非均衡性的特征，相互间的丰裕程度和职能分工促使各种要素的空间流动，反映了不同节点间的相互作用强度（王成金，2010）。距离衰减是形式或过程随距离减弱，可以反映流空间结构的整体特征。大量研究已证明距离衰减规律符合对数模式的Pareto 模型(式1)，可用于枢纽城市在各个距离段流动的频率分布累计率曲线的拟合。20世纪60年代，Tanner 和Sherratt 提出Tanner-Sherratt 模型（式2），可用于枢纽城市概率分布分配率曲线的拟合。

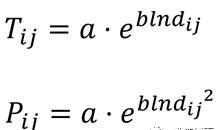
其中Tij为城市i在距离j的旅客流动数量的累积频率，a为系数，b为距离衰减系数。本例中将给出基于MATLAB的cftool工具箱进行帕累托距离衰减模型拟合的研究。枢纽城市旅客流的Pareto模型描述了旅客流在各个距离段的频率的累积速率，简言之就是曲线在某处越陡峭，则该枢纽城市在这个距离段内的目标城市旅客流动累积越快（就是说该枢纽城市跟分布在这个距离段的城市群之间的联系是紧密的），其实拟合出来的就是高数中提到的累积频率分布曲线。Pareto模型的改进版Tanner-Sherratt 模型则是定义各个枢纽城市的旅客流（出入流动均包括）在各个距离段的流动的分配率，其实拟合出来的就是高数中提到的概率分布函数的曲线。在本文我们不再区分二者，统一称为【帕累托距离衰减模型的拟合】。更多知识请参考王成金老师的论文《城际集装箱交流枢纽的识别及其物流特征——以中国铁路运输为例》，其中提出给了本例实验的理论支持和扩展阅读。本例实验中运用的原始数据来自于日本政府国土交通省官方网站上所公开的数据《日本全国纯流动调查》以及GIS环境中计算得到的加权平均距离。所有图表笔者都拥有最终解释权和版权，请勿擅自挪用。为防止纠纷，本文就不给出原始数据的分享链接了，还望谅解。有兴趣做类似研究的朋友可以仿照王成金老师的论文，根据自己研究中的情况，运用的OD数据来考察枢纽城市对周围城市辐射能力的距离衰减效果，相信本文的讲解会给读者朋友一定的参考价值。

dij为城市i在距离j的加权平均距离，根据日本国土交通省网站上所公布的1990年和2020年份的《旅客纯流动调查报告书》所估算的各个距离带（分界刻度为100km；200km；300km；500km；700km；1000km）中三大主流旅客运输方式（飞机，铁路或汽车）的贡献率为权重所计算的里程距离所求出的平均距离。具体细节可以参考论文Liu K., & Dauda T. S. (2020). Structural Changes in Japan’sUrban System from 1990 to 2010. Journal of Urban and Regional Analysis. 12(2),117-143.

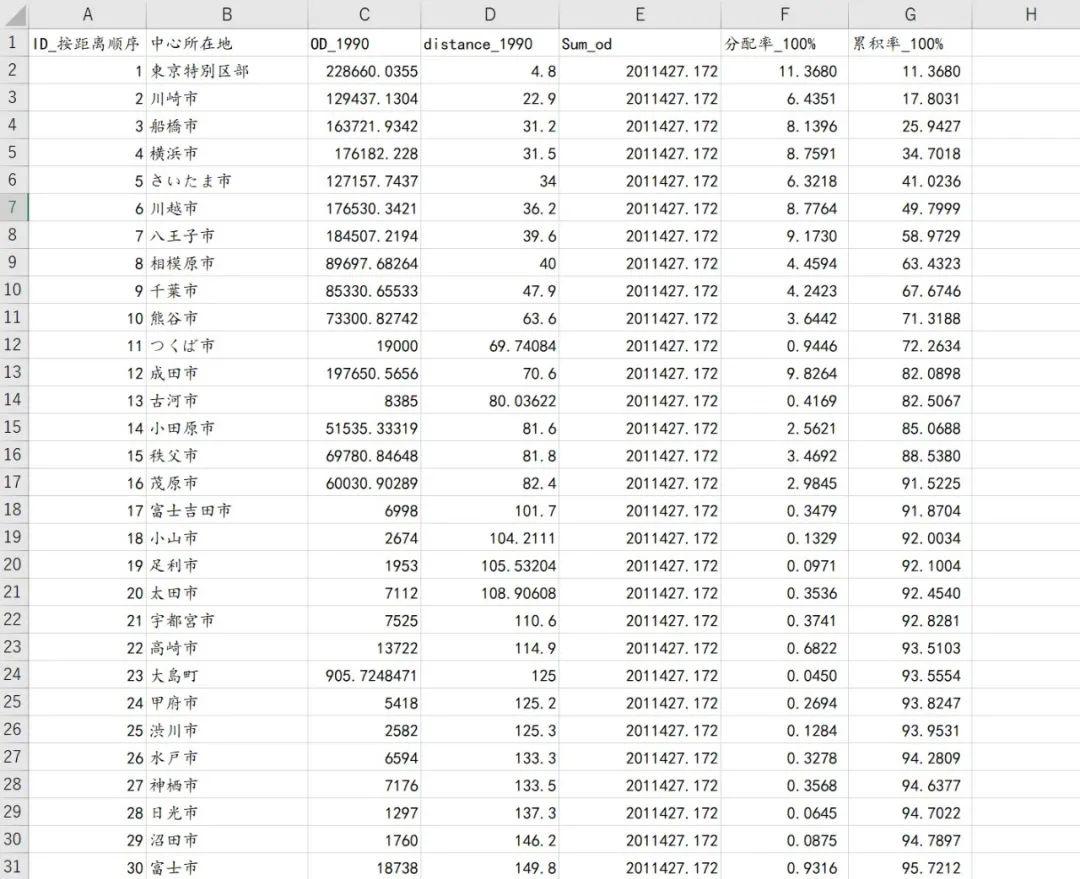
图5a

第二步，利用MATLAB的cftool工具箱进行帕累托距离衰减函数的曲线拟合（适用于几乎所有单变量的自定义函数）。首先载入原始数据（图5b）并定义好d（加权平均距离），T（累计频率百分率）和P（概率密度分配率）。建议实际操作过程中使用拖曳的方式或者load函数导入Excel数据。双击右上角的某一个变量即可查看内部表格。如图5b中命令窗口所示，输入d=Data(:,1);P=Data(:,3);T=Data(:,4);即可。

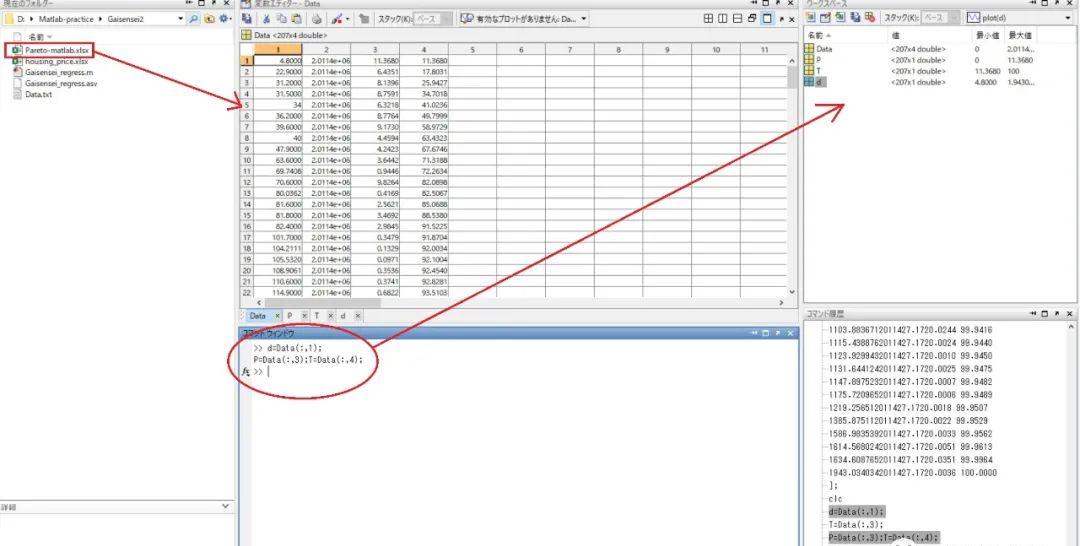
图5b

第三步，调用cftool工具包进行曲线拟合。命令窗口输入cftool即可弹出工具箱（见图5c）。数据Data→x数据选择d；y数据选择T→再单击创建数据集→关闭此对话框，即可看到散步图的预期视图。

图5c

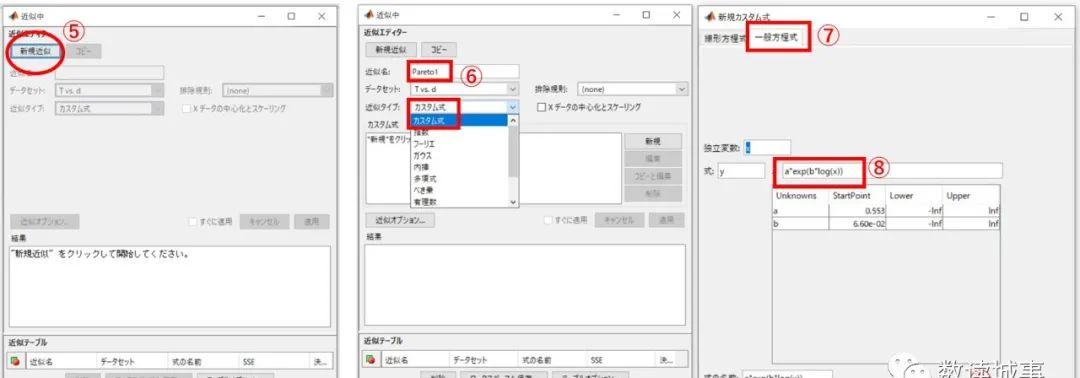
图5d

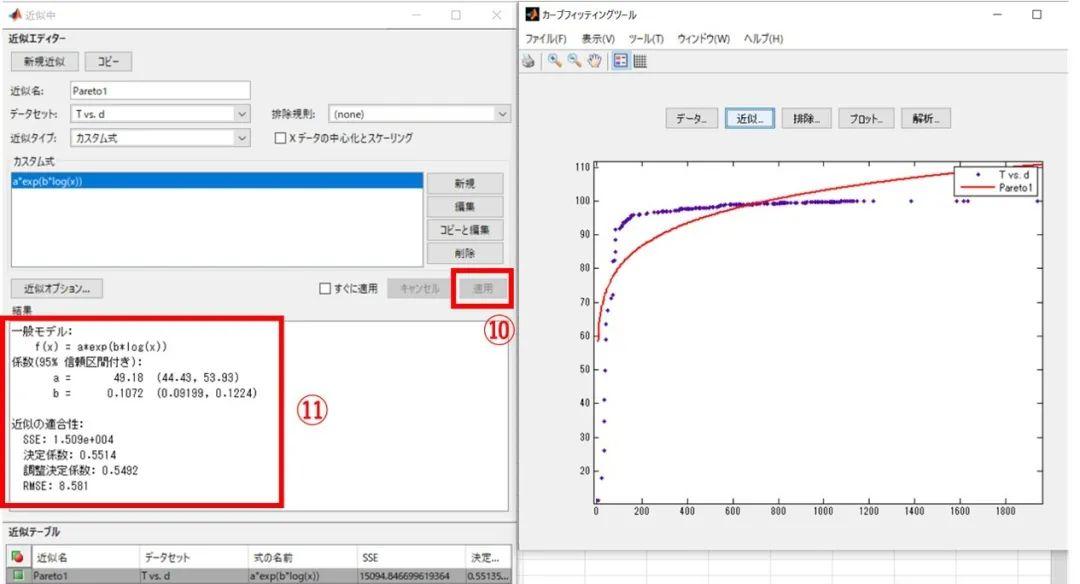
图5e

第四步，重复操作，拟合1990份其余城市的数据和2020年份的数据。原理相同，只需要换一套加载的数据即可。拟合Tanner-Sherratt 模型的话只需要在自定义函数的时候输入a*exp(b*log(x^2))即可。

我们可以根据MATLAB的计算结果（见图6a-6d）和GIS上生成的流动的空间模式以及其20年跨度的变化（见图7），来对日本七大地区各自所对应的枢纽城市的旅客流动的集散特征和距离衰减效果进行简单的解释。帕累托距离衰减函数的解释方法可以参考上文，如何在论文中展开科学论述的方法可以参考论文王成金（2010）和Liu & Dauda (2020)。

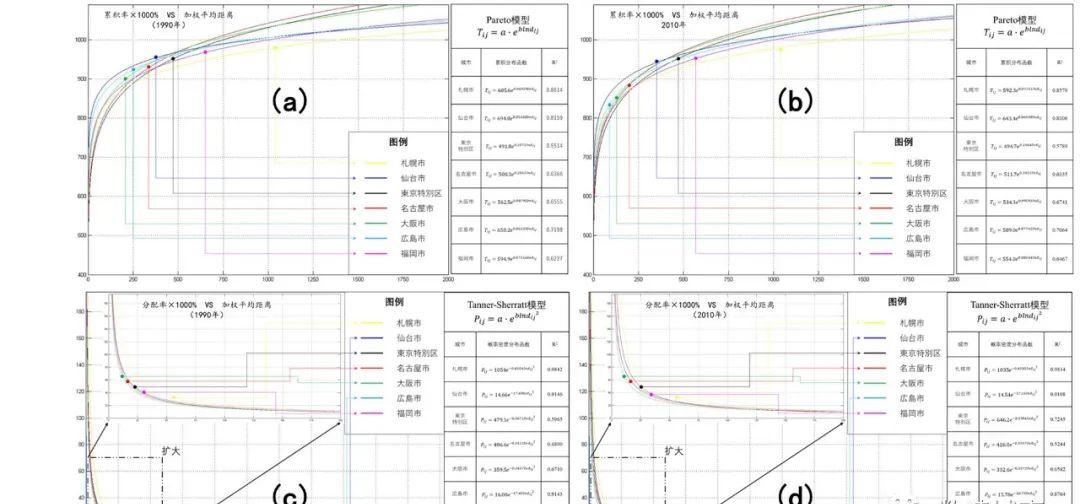
图6(a)—6(d)

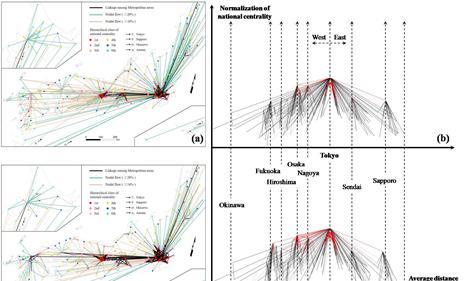
图7(a)—7(d)

【实例3】Logistic模型的拟合

Logistic模型y=1/(1 a*exp(-b*t)),在地理学的应用十分广泛，它的数学原理和适用研究例此文就不多作介绍。本例以美国城市化水平增长过程为例，基于MATLAB的glmfit函数说明二参数logistic模型的广义线性拟合方法。原始数据(图8)来自美国人口普查资料网站公布的美国城市化水平指数（即城市人口，乡村人口，总人口，城市化水平以及城乡人口比），见http：//www.census.gov/population。

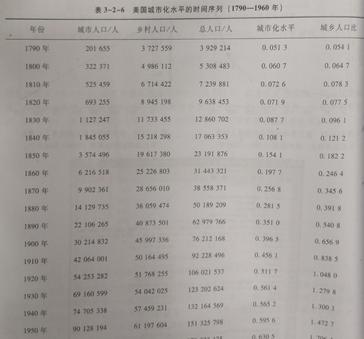图8

由于篇幅原因，glmfit函数的详细信息将不做出介绍，有兴趣的读者可以输入help glmfit查询。

代码过程的m文件见图9。第2-3行：导入数据，x代表年代，y代表城市化率。第4行：绘制散点图。第5行：保持图形。第6行：调用glmfit函数，函数模拟设定的【链接】指定缺省即可默认正态分布（样本的前提）。调用链接logit的意思就是指定拟合算法为自带的logistic模型。第7行：计算a和b的参数。第8行：计算预测值。第9行：绘制logistic拟合曲线。第10行：保持图形。第11行：计算标准误差。第12行：计算置信区间的上下限预测值。第13-14行：绘制上下限置信度的估计范围。第16行：输出各个参数：a=17.3533，b=0.0212，s=0.0278。从拟合曲线可以看出城市化率的曲线跟logistic模型契合的十分好。通过考察斜率的变化，或者跟其余城市的曲线做横向比较的话可能会有很有趣的结论，感兴趣的读者朋友可以做出尝试，本文在此就不赘述。

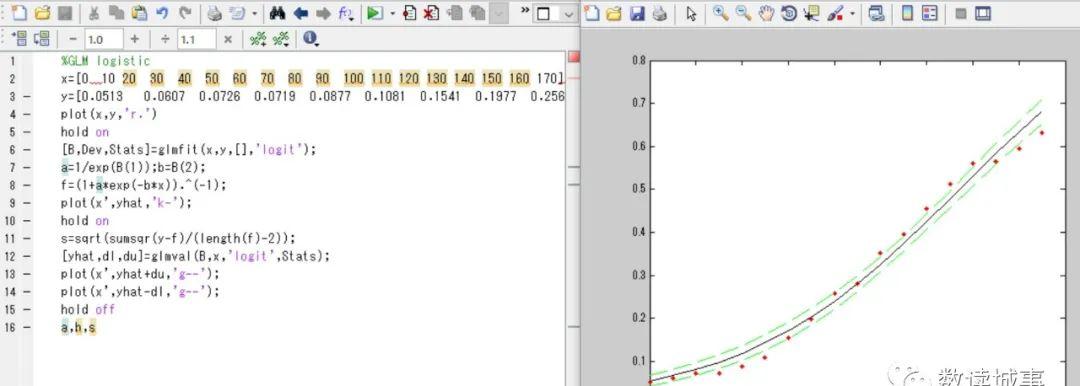
图9

【心得总结】

如何选取科学的模型呢？多读论文，并学会提炼问题与理解模型；学好统计学；多根据方法论整理地理学论文并思考如何对自己的研究产生参考意义；学会找到地理模型跟高等数学的接点；根据自己对编程语言或软件的掌握情况摸索出适合自己的教程（类似实例2）。

如何对结果进行科学地解释？多读论文，模仿论文中的语气；培养学术素养；多读图；仿照精品论文中的作图样式用于自己的研究。

【结语】

最后的结束语讲一下笔者的个人看法。关于统计学其实不必对所有的原理进行深入学习，只需要知道模型的原理、参数的含义、结果解释的方法以及如何根据结果将可信的结论转化成论文的语言即可。我们只需要懂得如何清洗和input数据、操作原理以及如何解释output数据，剩下的交给软件处理即可。我们其实并不需要拥有特别高深的技术或特别严密的数学证明，只需要打好专业基础，按需所学，“功利性”地带着目的去学习对自己有用的知识，形成自己的知识体系，但求从不求甚解到融会贯通，从略知一二到了如指掌，从生涩难懂到熟能生巧，从懵懂无知到自圆其说足矣。关于编程语言的学习，其实也是有很多套路的，我们只需要理清思路之后，根据自己的数据集合理地编写程序，如何实现之，如何合理地调用函数以及如何正确地编写程序（比如循环语句）就可以。笔者也曾有零基础的时期，当时正是一点点看书，一遍遍试错，慢慢调试，根据网上教程参考书籍并咨询专业人士慢慢提高编程水平的（虽然目前也只是初中级水平）。仿照精品论文中的作图样式用于自己的研究，即可达到自主编写程序的境界。只要坚持学习一段时间，你一定可以的。由于这是笔者第二次供稿，很多细节可能会有疏漏，如有建议或评论请在下方评论区互动，本期科研心得的介绍到此结束，谢谢大家的阅读！

【预告】

下一期，凯森赛将会介绍《基于MATLAB的矩阵运算与OD可视化》，敬请期待。